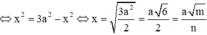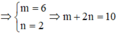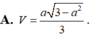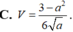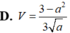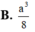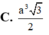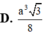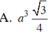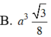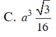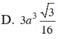Đáp án A
Phương pháp:
+) Chứng minh hình chiếu vuông của S trên (ABCD) trùng với tâm đường tròn ngoại tiếp tam giác ABD.
+) Chứng minh tam giác SAC vuông tại S, tính AC.
+) Tính BD.
+) Sử dụng công thức tính thể tích V S . A B C D = 1 3 S H . S A B C D = 1 3 S H . 1 2 A C . B D
Cách giải:
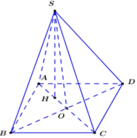
Vì SA = SB = SD = a nên hình chiếu vuông của S trên (ABCD) trùng với tâm đường tròn ngoại tiếp tam giác ABD.
Gọi H là tâm đường tròn ngoại tiếp tam giác ABD
⇒ S H ⊥ ( A B C D ) .
Do tam giác ABD cân tại A ⇒ H ∈ A C
Dễ dàng chứng minh được:
△ S B D = △ A B D ( c . c . c ) ⇒ S O = A O = A C 2 ⇒ △ S A C vuông tại S (Tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh ấy)
![]()
Áp dụng hệ thức lượng trong tam giác vuông SAC có S H = S A . S C A C = a x a 2 + x 2
Ta có
![]()
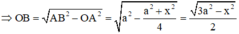
![]()
![]()
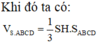
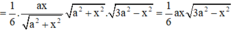
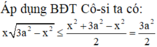
![]()
Dấu “=” xảy ra