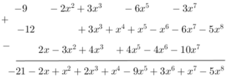x5 +4x3-6x2
A,4xy B,6x3 C,x5 D,4x2
B5
Những câu hỏi liên quan
thực hiện các phep tính sau:
a)3x3y2 : x2 b) (x5 + 4x3 – 6x2) : 4x2
c)10x3y – 5x2y2 – 25x4y3) : (-5xy) d) (27x3 – y3) : (3x – y)
\(a,=3xy^2\\ b,=\dfrac{1}{4}x^3+x-\dfrac{3}{2}\\ c,=-2x^2+xy+5x^3y^2\\ d,=\left(3x-y\right)\left(9x^2+3xy+y^2\right):\left(3x-y\right)=9x^2+3xy+y^2\)
Đúng 0
Bình luận (0)
x5=4x4+4x3+4x2+4x+5
\(\Leftrightarrow x^5-1=4x^4+4x^3+4x^2+4x+4\)
\(\Leftrightarrow\left(x-1\right)\left(x^4+x^3+x^2+x+1\right)=4\left(x^4+x^3+x^2+x+1\right)\)
\(\Leftrightarrow\left(x-5\right)\left(x^4+x^3+x^2+x+1\right)=0\)
\(\Leftrightarrow x=5\)
Đúng 1
Bình luận (0)
Cho
f
(
x
)
x
2
+
2
x
3
-
7
x
5
-
9
-
6
x
7
+
x
3
+
x
2
+
x
5
-
4
x
2
+...
Đọc tiếp
Cho
f ( x ) = x 2 + 2 x 3 - 7 x 5 - 9 - 6 x 7 + x 3 + x 2 + x 5 - 4 x 2 + 3 x 7 g ( x ) = x 5 + 2 x 3 - 5 x 8 - x 7 + x 3 + 4 x 2 - 5 x 7 + x 4 - 4 x 2 - x 6 - 12 h ( x ) = x + 4 x 5 - 5 x 6 - x 7 + 4 x 3 + x 2 - 2 x 7 + x 6 - 4 x 2 - 7 x 7 + x
Tính f(x) + g(x) – h(x)
Cho
f
(
x
)
x
2
+
2
x
3
-
7
x
5
-
9
-
6
x
7
+
x
3
+
x
2
+
x
5
-
4
x
2
+...
Đọc tiếp
Cho
f ( x ) = x 2 + 2 x 3 - 7 x 5 - 9 - 6 x 7 + x 3 + x 2 + x 5 - 4 x 2 + 3 x 7 g ( x ) = x 5 + 2 x 3 - 5 x 8 - x 7 + x 3 + 4 x 2 - 5 x 7 + x 4 - 4 x 2 - x 6 - 12 h ( x ) = x + 4 x 5 - 5 x 6 - x 7 + 4 x 3 + x 2 - 2 x 7 + x 6 - 4 x 2 - 7 x 7 + x
Thu gọn và sắp xếp các đa thức trên theo lũy thừa tăng của biến.
* f(x) = x2 + 2x3− 7x5 − 9 − 6x7 + x3 + x2 + x5 − 4x2 + 3x7
= (x2+ x2 – 4x2)+ (2x3 + x3 ) - (7x5 - x5 ) – 9 – (6x7 – 3x7)
= - 2x2 + 3x3 – 6x5 – 9 – 3x7
Sắp xếp theo thứ tự tăng của biến: f(x) = −9 − 2x2 + 3x3 − 6x5 − 3x7
* g(x) = x5 + 2x3 − 5x8 − x7 + x3 + 4x2 -5x7 + x4 − 4x2 − x6 – 12
= x5+ (2x3 + x3) - 5x8 – (x7+ 5x7) + (4x2 – 4x2 ) + x4 – x6 – 12
= x5 + 3x3 – 5x8 – 6x7 + x4 – x6 – 12
Sắp xếp theo thứ tự tăng của biến: g(x) = −12 + 3x3 + x4 + x5 – x6 − 6x7− 5x8
* h(x) = x + 4x5 − 5x6 − x7 + 4x3 + x2 − 2x7 + x6 − 4x2 − 7x7 + x.
= (x+ x) +4x5 – (5x6 – x6)- (x7 + 2x7+ 7x7) + 4x3+ (x2 – 4x2)
= 2x + 4x5 - 4x6 – 10x7 + 4x3 -3x2
Sắp xếp theo thứ tự tăng của biến: h(x) = 2x − 3x2 + 4x3 + 4x5 − 4x6 − 10x7
Đúng 0
Bình luận (0)
Bài 1:Thực hiện các phép tính
a. (x5 +4x3 - 6x2):4x2
b. (x3 +x2-12) : (x-2)
c. (-2x5+3x2-4x3):2x2
d. (x3 - 64):(x2 + 4x + 16)
Bài 2:Rút gọn biểu thức
a. 3x (x - 2)- 5x (1 - x) - 8(x2 - 3)
b.(x - y) (x2 + xy + y2)+2y3
c. (x - y)2 + (x+y)2 - 2(x-y) (x+y)
Đọc tiếp
Bài 1:Thực hiện các phép tính
a. (x5 +4x3 - 6x2):4x2
b. (x3 +x2-12) : (x-2)
c. (-2x5+3x2-4x3):2x2
d. (x3 - 64):(x2 + 4x + 16)
Bài 2:Rút gọn biểu thức
a. 3x (x - 2)- 5x (1 - x) - 8(x2 - 3)
b.(x - y) (x2 + xy + y2)+2y3
c. (x - y)2 + (x+y)2 - 2(x-y) (x+y)
a) \(\left(x^5+4x^3-6x^2\right):4x^2\)
\(=\left(x^5:4x^2\right)+\left(4x^3:4x^2\right)+\left(-6x^2:4x^2\right)\)
\(=\dfrac{1}{4}x^3+x-\dfrac{3}{2}\)
b)
Vậy \(\left(x^3+x^2-12\right):\left(x-2\right)=x^2+3x+6\)
c) (-2x5 : 2x2) + (3x2 : 2x2) + (-4x^3 : 2x^2)
= \(-x^3+\dfrac{3}{2}-2x\)
d) \(\left(x^3-64\right):\left(x^2+4x+16\right)\)
\(=\left(x-4\right)\left(x^2+4x+16\right):\left(x^2+4x+16\right)\)
\(=x-4\)
(dùng hẳng đẳng thức thứ 7)
Bài 2 :
a) 3x(x - 2) - 5x(1 - x) - 8(x2 - 3)
= 3x2 - 6x - 5x + 5x2 - 8x2 + 24
= (3x2 + 5x2 - 8x2) + (-6x - 5x) + 24
= -11x + 24
b) (x - y)(x2 + xy + y2) + 2y3
= x3 - y3 + 2y3
= x3 + y3
c) (x - y)2 + (x + y)2 - 2(x - y)(x + y)
= (x - y)2 - 2(x - y)(x + y) + (x + y)2
= [(x - y) + x + y)2 = [x - y + x + y] = (2x)2 = 4x2
Đúng 0
Bình luận (0)
Bài 1 :
a]= \(\frac{1}{4}\)x3 + x - \(\frac{3}{2}\).
b] => [x3 + x2 -12 ] = [ x2 +3 ][x-2] + [-6]
c]= -x3 -2x +\(\frac{3}{2}\).
d] = [ x3 - 64 ] = [ x2 + 4x + 16][ x- 4].
Cho f(x) x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7; g(x) x4 + 4x3 − 5x8 − x7 + x3 + x2 − 2x7 + x4 – 4x2 − x8. Thu gọn và sắp xếp các đa thức f(x) và g(x) theo luỹ thừa giảm của biến rồi tìm bậc của đa thức đó.
Đọc tiếp
Cho f(x)= x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7; g(x) = x4 + 4x3 − 5x8 − x7 + x3 + x2 − 2x7 + x4 – 4x2 − x8. Thu gọn và sắp xếp các đa thức f(x) và g(x) theo luỹ thừa giảm của biến rồi tìm bậc của đa thức đó.
f(x) = x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7
= (x5 + x5) + (3x2 + 2x2 – 4x2) + (-5x3 + x3) + (-x7 + x7)
= 2x5 + x2 – 4x3.
= 2x5 - 4x3 + x2
Đa thức có bậc là 5
g(x) = x4 + 4x3 – 5x8 – x7 + x3 + x2 – 2x7 + x4 – 4x2 – x8
= (x4 + x4) + (4x3 + x3) – (5x8 + x8) – (x7 + 2x7) + (x2 – 4x2)
= 2x4 + 5x3 – 6x8 – 3x7 – 3x2
= -6x8 - 3x7 + 2x4 + 5x3 - 3x2.
Đa thức có bậc là 8.
Đúng 0
Bình luận (0)
Đa thức có bậc là 5 nhe
Phân tích các đa thức sau thành nhân tử:
a) A= \(x^3\)y - 12xy - x2y
b)B= 4x2 - 3y2 - 4xy - 2x + 3y
c)C= (x+1)(x+2)(x+3)(x+4) - 120
d)D= x5 - x4 + x2 - 1
a: \(A=x^3y-12xy-x^2y\)
\(=xy\cdot x^2-xy\cdot12-xy\cdot x\)
\(=xy\left(x^2-x-12\right)\)
\(=xy\left(x^2-4x+3x-12\right)\)
\(=xy\left[x\left(x-4\right)+3\left(x-4\right)\right]\)
\(=xy\left(x-4\right)\left(x+3\right)\)
c: \(C=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-120\)
=(x+1)(x+4)(x+2)(x+3)-120
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-120\)
\(=\left(x^2+5x\right)^2+10\left(x^2+5x\right)+24-120\)
\(=\left(x^2+5x\right)^2+10\left(x^2+5x\right)-96\)
\(=\left(x^2+5x+16\right)\left(x^2+5x-6\right)\)
\(=\left(x^2+5x+16\right)\left(x+6\right)\left(x-1\right)\)
d: \(D=x^5-x^4+x^2-1\)
\(=\left(x^5-x^4\right)+\left(x^2-1\right)\)
\(=x^4\left(x-1\right)+\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(x^4+x+1\right)\)
Đúng 2
Bình luận (1)
Bài 7: Chứng minh rằng các đa thức sau là bình phương của một đa thứca.A x4+ 4x3+ 2x2– 4x + 1Gợi ý: giảsử: x4+ 4x3+ 2x2–4x + 1 (ax2+ bx + c).(ax2+ bx + c)Tính vế phải và đồng nhất hệ số với vế trái b.B x4-6x3+ 19x2–30x + 25c.C 4x2+ y2–4xy + 8x –4y + 4 Giúp mình gấp với ạ!
Đọc tiếp
Bài 7: Chứng minh rằng các đa thức sau là bình phương của một đa thức
a.A = x4+ 4x3+ 2x2– 4x + 1
Gợi ý: giảsử: x4+ 4x3+ 2x2–4x + 1= (ax2+ bx + c).(ax2+ bx + c)
Tính vế phải và đồng nhất hệ số với vế trái
b.B = x4-6x3+ 19x2–30x + 25
c.C = 4x2+ y2–4xy + 8x –4y + 4
Giúp mình gấp với ạ!
c) Ta có: \(C=4x^2+y^2-4xy+8x-4y+4\)
\(=\left(2x-y\right)^2+2\cdot\left(2x-y\right)\cdot2+2^2\)
\(=\left(2x-y+2\right)^2\)
Đúng 1
Bình luận (1)
Phân tích đa thức thành nhân tử :
a.x4 - 4x3 + 11x2 - 16x + 16
b.x4 + 6x3 + 13x2 + 12x + 4
c.x4 + x3 - 4x2 + x + 1
d.x4 + x3 - 4x2 + x + 1
c: \(x^4+x^3-4x^2+x+1\)
\(=x^4-x^3+2x^3-2x^2-2x^2+2x-x+1\)
\(=\left(x-1\right)\left(x^3+2x^2-2x-1\right)\)
\(=\left(x-1\right)\left[\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\right]\)
\(=\left(x-1\right)^2\cdot\left(x^2+3x+1\right)\)
Đúng 2
Bình luận (0)