Giải phương trình sin 2 x + sin 2 3 x + sin 2 5 x = 3 2
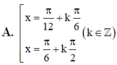
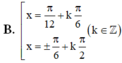
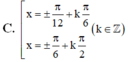
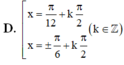
giải phương trình sin^2 x − 4√3 sin x · cos x + cos^2 x = −2.
Với \(cosx=0\) ko phải nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow tan^2x-4\sqrt{3}tanx+1=-2\left(1+tan^2x\right)\)
\(\Leftrightarrow3tan^2x-4\sqrt{3}tanx+3=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x=\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2)
B. (1)
C. (3)
D. (1) và (2)
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2).
B. (1).
C. (3).
D. (1) và (2).
Chọn C
Ta có: ![]() nên (1) và (2) có nghiệm.
nên (1) và (2) có nghiệm.
Cách 1:
Xét: ![]()
![]() nên (3) vô nghiệm.
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 

nên (3) vô nghiệm.
a) Giải phương trình: \(\sin x = \frac{{\sqrt 3 }}{2}\)
b) Tìm góc lượng giác x sao cho \(\sin x = \sin {55^ \circ }\)
a) \(\sin x = \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin x = \sin \frac{\pi }{3} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \pi - \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.\)
b) \(\begin{array}{l}\sin x = \sin {55^ \circ } \Leftrightarrow \left[ \begin{array}{l}x = {55^ \circ } + k{.360^ \circ }\\x = {180^ \circ } - {55^ \circ } + k{.360^ \circ }\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = {55^ \circ } + k{.360^ \circ }\\x = {125^ \circ } + k{.360^ \circ }\end{array} \right.\\\end{array}\)
Giải các phương trình sau :
a) \(\cos^2x+2\sin x\cos x+5\sin^2x=2\)
b) \(3\cos^2x-2\sin2x+\sin^2x=1\)
c) \(4\cos^2x-3\sin x\cos x+3\sin^2x=1\)
Giải các phương trình sau. π 1. 2sin( x − ) − 2 = 0 . 4 2. sin 2 x − 2 3 sin 2 x − cos x + 3 sin x = 0 .
giúp em với adim
lớp 11
Giải các phương trình sau :
a) \(2\sin^2x+\sin x\cos x-3\cos^2x=0\)
b) \(3\sin^2-4\sin x\cos x+5\cos^2x=2\)
c) \(\sin^2x+\sin2x-2\cos^2+5\cos^2x=2\)
d) \(2\cos^2x-3\sqrt{3}\sin2x-4\sin^2x=-4\)
a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; ![]() }.
}.
Vậy ![]()
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan3 + kπ, k ∈ Z.
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; ![]() =
= ![]() (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
(sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
![]() sin2x + 2sinxcosx -
sin2x + 2sinxcosx - ![]() cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan(-5) + kπ, k ∈ Z.
+ kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 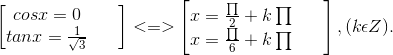
giải phương trình: sin(2x+pi/2)=sin(x-pi/3)
\(sin\left(2x+\dfrac{\Omega}{2}\right)=sin\left(x-\dfrac{\Omega}{3}\right)\)
=>\(\left[{}\begin{matrix}2x+\dfrac{\Omega}{2}=x-\dfrac{\Omega}{3}+k2\Omega\\2x+\dfrac{\Omega}{2}=\Omega-x+\dfrac{\Omega}{3}+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{5}{6}\Omega+k2\Omega\\3x=\dfrac{4}{3}\Omega-\dfrac{1}{2}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{5}{6}\Omega+k2\Omega\\x=\dfrac{5}{18}\Omega+\dfrac{k2\Omega}{3}\end{matrix}\right.\)
giải phương trình: sin(2x+pi/2)=sin(x-pi/3)
Lời giải:
$\sin (2x+\frac{\pi}{2})=\sin (x-\frac{\pi}{3})$
\(\Rightarrow \left[\begin{matrix}\ 2x+\frac{\pi}{2}=x-\frac{\pi}{3}+2k\pi\\ 2x+\frac{\pi}{2}=\pi -(x-\frac{\pi}{3})+2k\pi\end{matrix}\right.\)
\(\Rightarrow \left[\begin{matrix}\ x=\pi (2k-\frac{5}{6})\\ x=\frac{1}{3}\pi (\frac{5}{6}+2k)\end{matrix}\right.\) với $k$ nguyên bất kỳ.
Giải các phương trình sau:
\(5\sin^22x-6\sin4x-2\cos^2x=0\)
\(2\sin^23x-10\sin6x-\cos^23x=-2\)
\(\sin^2x\left(\tan x+1\right)=3\sin x\left(\cos x-\sin x\right)+3\)
\(6\sin x-2\cos^3x=\frac{5\sin4x.\cos x}{2\cos2x}\)