Cho hai đường thẳng d : x - 1 2 = y + 1 3 = z - 5 1 , d ' : x - 1 3 = y + 2 2 = z + 1 2 . Vị trí tương đối của d và d’ là
A. Chéo nhau
B. Song song
C. Cắt nhau
D. Trùng nhau
PB
Những câu hỏi liên quan
Bài 14 Cho parabol P y x 2 và đường thẳng d y 2m 1 x m 3 . Tìm m d hat e P và d cắt nhau tại hai điểm A, B nằm bên phải trục tùng, Bài 15 Cho parabol P y x 2 và đường thẳng d y a 1 x a . Tim a để P và d cắt nhau tại hai điểm phân biệt A và B sao cho tam giác AOB Bài 16 Cho Parabol P y x 2 và đường thẳng d y m 1 x m m là tham số . vuông tại O. Tim m d hat e đường thẳng d cắt parabol P tại hai điểm P và Q sao cho t...
Đọc tiếp
Bài 14 Cho parabol P y x 2 và đường thẳng d y 2m 1 x m 3 . Tìm m d hat e P và d cắt nhau tại hai điểm A, B nằm bên phải trục tùng, Bài 15 Cho parabol P y x 2 và đường thẳng d y a 1 x a . Tim a để P và d cắt nhau tại hai điểm phân biệt A và B sao cho tam giác AOB Bài 16 Cho Parabol P y x 2 và đường thẳng d y m 1 x m m là tham số . vuông tại O. Tim m d hat e đường thẳng d cắt parabol P tại hai điểm P và Q sao cho tam giác OPQ vuông tại Q.
Trên mặt phẳng toại độ Oxy, cho đường thẳng (d):y=(m-1)x-m với m là tham số.
Tìm m để (d) đồng quy với hai đường thẳng (d'):y=x - `2/3` và (d''):y=-x+1
Tọa độ giao điểm của (d') với (d'') là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}x-\dfrac{2}{3}=-x+1\\y=-x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+x=\dfrac{2}{3}+1\\y=-x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=\dfrac{5}{3}\\y=-x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}\\y=-\dfrac{5}{6}+1=\dfrac{1}{6}\end{matrix}\right.\)
Thay x=5/6 và y=1/6 vào (d), ta được:
\(\dfrac{5}{6}\left(m-1\right)-m=\dfrac{1}{6}\)
=>\(\dfrac{5}{6}m-\dfrac{5}{6}-m=\dfrac{1}{6}\)
=>\(-\dfrac{1}{6}m=1\)
=>m=-1:1/6=-6
Đúng 2
Bình luận (0)
cho hai dường thẳng d :y=(m^2-3m+5)x+m-1 và đường thẳng d':y=(m=2)x+5-m,tìm m để hai đương thẳng song song với nhau
Để 2 đường thẳng d và d' song song với nhau thì
\(\left\{{}\begin{matrix}m^2-3m+5=m+2\\m-1\ne5-m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-4m+3=0\\2m\ne6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(m-3\right)=0\\m\ne3\end{matrix}\right.\)
\(\Leftrightarrow m=1\left(tm\right)\)
Đúng 0
Bình luận (0)
Cho hai đường thẳng :
(d 1 ) : y = - 3x + m + 1
(d 2 ) : y = ( 2k + 6 ) x + 2 – m ( k ≠ - 3 )
a) Xác định k, m để hai đường thẳng trùng nhau
b) Xác định k, m để hai đường thẳng song song
c) Xác định k, m để hai đường thẳng cắt nhau
d) Xác định k, m để hai đường thẳng vuông góc với nhau
Để 2 đường thẳng trùng nhau \(\Rightarrow\left\{{}\begin{matrix}2k+6=-3\\2-m=m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=-\frac{9}{2}\\m=\frac{1}{2}\end{matrix}\right.\)
Để 2 đường thẳng song song \(\Rightarrow\left\{{}\begin{matrix}2k+6=-3\\2-m\ne m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=-\frac{9}{2}\\m\ne\frac{1}{2}\end{matrix}\right.\)
Để 2 đường thẳng cắt nhau \(\Rightarrow2k+6\ne-3\Rightarrow k\ne-\frac{9}{2}\)
Để 2 đường thẳng vuông góc \(\Rightarrow\left(2k+6\right).\left(-3\right)=1\Rightarrow k=-\frac{19}{6}\)
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d
1
:
x
-
1
2
y
-
1
-
1
z
+
1
1
,
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d 1 : x - 1 2 = y - 1 - 1 = z + 1 1 , d 2 : x + 2 3 = y + 1 1 = z - 2 2 Đường thẳng đi qua điểm M và cắt cả hai đường thẳng d₁, d₂ tại hai điểm A, B. Độ dài đoạn thẳng AB bằng:
A. √38
B. 2√10
C. 8
D. 12
Chọn A
Vì A thuộc 
nên A (1+2t;1-t;-1+t).
Vì B thuộc 
nên B (-2+3t';-1+t';2+2t').
Thay vào (3) ta được t=1, t'=2 thỏa mãn.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai đường thẳng d₁ và d₂ lần lượt có phương trình là
x
1
y
+
1
2
z
1
v
à
x
1
y
-
1
-
2...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d₁ và d₂ lần lượt có phương trình là x 1 = y + 1 2 = z 1 v à x 1 = y - 1 - 2 = z - 1 3 .Đường thẳng d cắt cả hai đường thẳng d₁, d₂ và song song với đường thẳng ∆ : x - 4 1 = y - 7 4 = z - 3 - 2 có phương trình là:
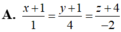
Chọn B
Gọi (P) là mặt phẳng chứa hai đường thẳng d₁ và d₂
Khi đó (P) đi qua M (0;-1;0) và có cặp véctơ chỉ phương 
Gọi 
là VTPT của (P). Khi đó 
Phương trình (P): -8x+3y+2z+3=0
Gọi H là giao điểm của đường thẳng d₂ và (P):
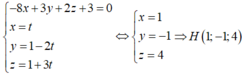
Đường thẳng d đi qua H và có VTCP 
có phương trình:
Đúng 0
Bình luận (0)
Bài 3
Cho hàm số bậc nhất y = (m – 2)x + 2 – m với m là tham số, có đồ thị là đường thẳng d.
1) Vẽ đường thẳng d trên mặt phẳng tọa độ Oxy với m = 3
2) Cho hai đường thẳng d1: y = x + 2 và d2: y = 4 – 3x. Tìm m để ba đường thẳng d, d1, d2 đồng quy.
2: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=4-3x\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=1/2 và y=5/2 vào (d), ta được:
\(\dfrac{1}{2}m-1+2-m=\dfrac{5}{2}\)
=>-1/2m=3/2
hay m=-3
Đúng 1
Bình luận (0)
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
Cho hai đường thẳng d và d'. Tìm m để hai đường thẳng: cắt nhau, song song, đồng quy
a) d: 2mx+(m-1).y-2=0, d': (m+2).x+(2m+1).y-(m+2)=0
b) d: (m-2).x+(m-6).y+m-1=0, d': (m-4).x+(2m-3).y+m-5=0
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d:
x
1
y
-
2
z
+
1
1
và d
x
-
1
-
2
)...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d: x 1 = y - 2 = z + 1 1 và d'= x - 1 - 2 ) = y - 2 4 = z 2 . Viết phương trình mặt phẳng (Q) chứa hai đường thẳng d và d’
A. Không tồn tại (Q)
B. (Q): y-2z-2= 0
C. (Q): x-y-2= 0
D. (Q):-2y+4z+1= 0
