Cho dãy số ( u n ) được xác định như sau u 1 = 2019 ; u n + 1 = u n 2 + 1 .Khi đó u 10 bằng ( làm tròn đến bốn số thập phân sau dấu phẩy)
A. 45,0333
B. 45,0222
C. 45,0444
D. 45, 0555
Cho dãy số thực (un) xác định bởi \(\left\{{}\begin{matrix}u_1=2019\\u^2_n+2018u_n-2020u_{n+1}+1=0\left(n\in N\cdot\right)\end{matrix}\right.\). Tìm giới hạn của dãy số (Sn), biết: Sn = \(\dfrac{1}{u_1+2019}+\dfrac{1}{u_2+2019}+...+\dfrac{1}{u_n+2019}\)
Đề không cho sẵn dãy tăng à? Vậy phải chứng minh nó tăng trước
\(u_{n+1}=\dfrac{u_n^2+2018u_n+1}{2020}\)
\(u_{n+1}-u_n=\dfrac{u_n^2+2018u_n+1}{2020}-u_n=\dfrac{\left(u_n-1\right)^2}{2020}\ge0\) \(\Rightarrow\) dãy tăng và không bị chặn trên \(\Rightarrow lim\left(u_n\right)=+\infty\)
\(\Rightarrow2020u_{n+1}=u_n^2+2018u_n+1\)
\(\Leftrightarrow2020u_{n+1}-2020=u_n^2+2018u_n-2019\)
\(\Leftrightarrow2020\left(u_{n+1}-1\right)=\left(u_n+2019\right)\left(u_n-1\right)\)
\(\Rightarrow\dfrac{1}{2020\left(u_{n+1}-1\right)}=\dfrac{1}{\left(u_n+2019\right)\left(u_n-1\right)}=\dfrac{1}{2020}\left(\dfrac{1}{u_n-1}-\dfrac{1}{u_n+2019}\right)\)
\(\Rightarrow\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Thế n=1;2;...;n ta được:
\(\dfrac{1}{u_1+2019}=\dfrac{1}{u_1-1}-\dfrac{1}{u_2-1}\)
\(\dfrac{1}{u_2+2019}=\dfrac{1}{u_2-1}-\dfrac{1}{u_3-1}\)
...
\(\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Cộng vế: \(S_n=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}=\dfrac{1}{2018}-\dfrac{1}{u_{n+1}-1}\)
\(\Rightarrow\lim\left(S_n\right)=\dfrac{1}{2018}-\dfrac{1}{\infty}=\dfrac{1}{2018}\)
Cho dãy số \((u_n)\) được xác định : \(\left\{ \begin{array}{l} {u_1} = 2019\\ {u_n} = - \frac{{2019}}{n}({u_1} + {u_2} + ... + {u_{n - 1}}),n > 1 \end{array} \right.\) .Tính \(T = 2{u_1} + {2^2}{u_2} + ... + {2^{2019}}{u_{2019}}\)
Cho dãy số (un) được xác định như sau: u1= 2017; un-1= n2(un-1 - un) với mọi n ∈ N*, n ≥2. Tìm giới hạn dãy số (un)
Lời giải:
$\frac{u_{n-1}}{u_n}=\frac{n^2}{n^2-1}>0$ với mọi $n\geq 2$ nên $u_{n-1}, u_n$ luôn cùng dấu.
Mà $u_1=2017>0$ nên $u_n>0$ với mọi $n=1,2,...$
Mặt khác:
$n^2(u_{n-1}-u_n)=u_{n-1}>0\Rightarrow u_{n-1}>u_n$ nên dãy $(u_n)$ là dãy giảm.
Dãy giảm và bị chặn dưới nên $u_n$ hội tụ. Đặt $\lim u_n=a$.
Ta có: $a=n^2(a-a)\Rightarrow a=0$
Vậy $\lim u_n=0$
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Chọn A
Phương pháp: Tìm công thức số hạng tổng quát
Cách giải: Ta có:
u ( 1 ) = 1
u ( 2 ) = u ( 1 ) + u ( 1 ) = 2 u ( 1 ) + 1
u ( 3 ) = u ( 2 ) + u ( 1 ) = 3 u ( 1 ) + 1 + 2
u ( 4 ) = u ( 3 ) + u ( 1 ) = 4 u ( 1 ) + 1 + 2 + 3
. . .
u ( 2017 ) = u ( 2016 ) + u ( 1 ) = 2017 u ( 1 ) + 1 + 2 + 3 . . . + 2016
⇒ u ( 2017 ) = 1 + 2 + 3 . . . + 2016 + 2017 = 2035153
Cho dãy số (un) được xác định như sau: u 1 = 1 u n = 3 u n - 1 + 1 2 u n - 1 - 2 , n ≥ 2 Viết 4 số hạng đầu của dãy và chứng minh rằng un > 0, ∀ n
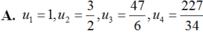
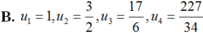
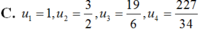
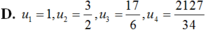
Chọn B.
Ta có: u1 = 1; u2 = 3/2; u3 = 17/6; u4 = 227/34.
Ta chứng minh un > 0 bằng quy nạp.
Giả sử un > 0, khi đó: 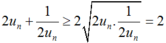
Nên 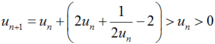 .
.
Cho dãy Un được xác định như sau: U1=1; U2=2;U3=3 và Un+3= 2Un+2-3Un+1+2Un
a) Viết quy trình bấm phím liên tục để tính Un\(\left(n\ge4\right)\)
b) Tính U19;U20
Cho dãy số u n được xác định như sau: u 1 = 2 u n + 1 + 4 u n = 4 − 5 n n ≥ 1 .
Tính tổng S = u 2018 − 2 u 2017 .
A. S = 2015 − 3.4 2017
B. S = 2016 − 3.4 2018
C. S = 2016 + 3.4 2018
D. S = 2015 + 3.4 2017
Cho dãy số (Un) được xác định như sau: \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\). Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó
Cho dãy số (Un) được xác định như sau \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\) . Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó