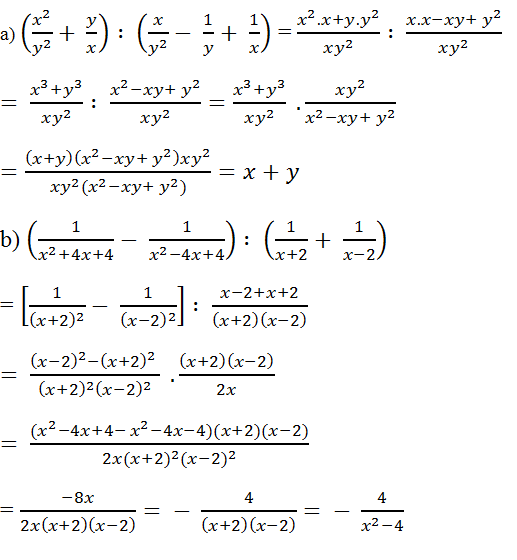Làm phép tính sau: x 2 y 2 + y x : x y 2 - 1 y + 1 x
PB
Những câu hỏi liên quan
Thực hiện phép tính sau:
x+y/2(x-y) - x-y/2(x+y) + 2y2/x2y2
làm nhanh mk tick ạ.
Làm các phép tính sau :
a) \(\left(\dfrac{x^2}{y^2}+\dfrac{y}{x}\right):\left(\dfrac{x}{y^2}-\dfrac{1}{y}+\dfrac{1}{x}\right)\)
b) \(\left(\dfrac{1}{x^2+4x+4}-\dfrac{1}{x^2-4x+4}\right):\left(\dfrac{1}{x+2}-\dfrac{1}{x-2}\right)\)
làm tính trừ \(\dfrac{5x+y}{xy-5x^2}\)-\(\dfrac{35x^2+8xy+y^2}{xy^225x^3}\)
thực hiện phép tính \(\dfrac{x^3+6x^2-25}{x^3+3x^2-10x}\)-\(\dfrac{x+5}{2x-x^2}\)
b: \(=\dfrac{x^3+6x^2-25}{x\left(x+5\right)\left(x-2\right)}+\dfrac{x+5}{x\left(x-2\right)}\)
\(=\dfrac{x^3+6x^2-25+x^2+10x+25}{x\left(x+5\right)\left(x-2\right)}=\dfrac{x^3+7x^2+10x}{x\left(x+5\right)\left(x-2\right)}=\dfrac{x+2}{x-2}\)
Đúng 1
Bình luận (0)
làm phép tính 4(x-3y)(x+3y)+(2y-y)2
làm các phép tính sau
a,y/2x2-xy + 4x/y2-2xy
b,1/x+2 + 3/x2-4 + x-14/(x2+4x+4) (x-2)
c,1/x+2 + 1/(x+2)(4x+7)
d,1/x+3 + 1/(x+3) (x+2) + 1/(x+2)(4x+7)
Bài 1: Làm phép chia
( - 2 x^5 y)^8 : ( - 2 x^5 y)^6
Bài 2: Làm tính chia
[ (2x-y)^7 - 6.(2x-y)^5 - (y-2x)^4 + (y-2x)^3 ] :(2x-y)^3
5-/2x+6/-/7-y/
Bài 1: Làm phép chia
( - 2 x^5 y)^8 : ( - 2 x^5 y)^6
Bài 2: Làm tính chia
[ (2x-y)^7 - 6.(2x-y)^5 - (y-2x)^4 + (y-2x)^3 ] :(2x-y)^3
bài 1:
(-2x^5 y)^8:(-2x^5 y)^6
=(-2x^5 y)^8-6
=(-2x^5y)^2
=4x^25 y^2
Đúng 0
Bình luận (0)
thực hiện phép tính sau\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)
MTC = (x - y)(x2 + xy + y2)
\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)
\(=\dfrac{x^2+xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{3xy}{\left(x-y\right)\left(x^2+xy+y^2\right)}+\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2x^2-4xy+2y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)
Đúng 1
Bình luận (0)
1/x-y-3xy/x^3-y^3+x-y/x^2+xy+y^2
=1/x-y+-3xy/(x-y)(x^2+xy+y^2)+x-y/x^2+xy+y^2
=x^2+xy+y^2/(x-y)(x^2+xy+y^2)+-3xy/(x-y)(x^2+xy+y^2)+x^2-2xy+y^2/(x-y)(x^2+xy+y^2)
=x^2+xy+y^2-3xy+x^2-2xy-y^2/(x-y)(x^2+xy+y^2)
=2x^2-5xy/(x-y)(x^2+xy+y^2)
Đúng 0
Bình luận (0)
MTC = (x - y)(x2 + xy + y2)
\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)
\(=\dfrac{x^2+xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{3xy}{\left(x-y\right)\left(x^2+xy+y^2\right)}+\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2x^2-4xy+2y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)
Đúng 0
Bình luận (0)
Thực hiện phép tính sau:
\(\dfrac{3}{2x^2+y}+\dfrac{5}{xy^2}+\dfrac{x}{y^3}\)
\(\dfrac{3}{2x^2+y}+\dfrac{5}{xy^2+}+\dfrac{x}{y^3}\)
=\(\dfrac{3xy^5}{xy^2.y^3\left(2x^2+y\right)+}+\dfrac{10y^3x^2+5y^4}{xy^2.y^3\left(2x^2+y\right)}+\dfrac{2x^4y^2+x^2y^3}{xy^2.y^3\left(2x^2+y\right)}\)
=\(\dfrac{3xy^5+10y^3x^2+5y^4+2x^4y^2+x^2y^3}{xy^5\left(2x^2+y\right)}\)
=\(\dfrac{3xy^5+11y^3x^2+5y^4+2x^4y^2}{xy^5\left(2x^2+y\right)}\)
ủa đáp án cứ sao sao:<
Đúng 0
Bình luận (0)
Thực hiện phép tính sau:
\(\frac{xy}{x-y}-\frac{2x^2}{y-2x}\)
\(\dfrac{xy}{x-y}-\dfrac{2x^2}{y-2x}\)
\(=\dfrac{xy}{x-y}+\dfrac{2x^2}{2x-y}\)
\(=\dfrac{xy\left(2x-y\right)+2x^2\left(x-y\right)}{\left(x-y\right)\left(2x-y\right)}\)
\(=\dfrac{2x^2y-xy^2+2x^3-2x^2y}{\left(x-y\right)\left(2x-y\right)}\)
\(=\dfrac{2x^3-xy^2}{\left(x-y\right)\left(2x-y\right)}=\dfrac{x\left(2x^2-y^2\right)}{\left(x-y\right)\left(2x-y\right)}\)
Đúng 2
Bình luận (0)