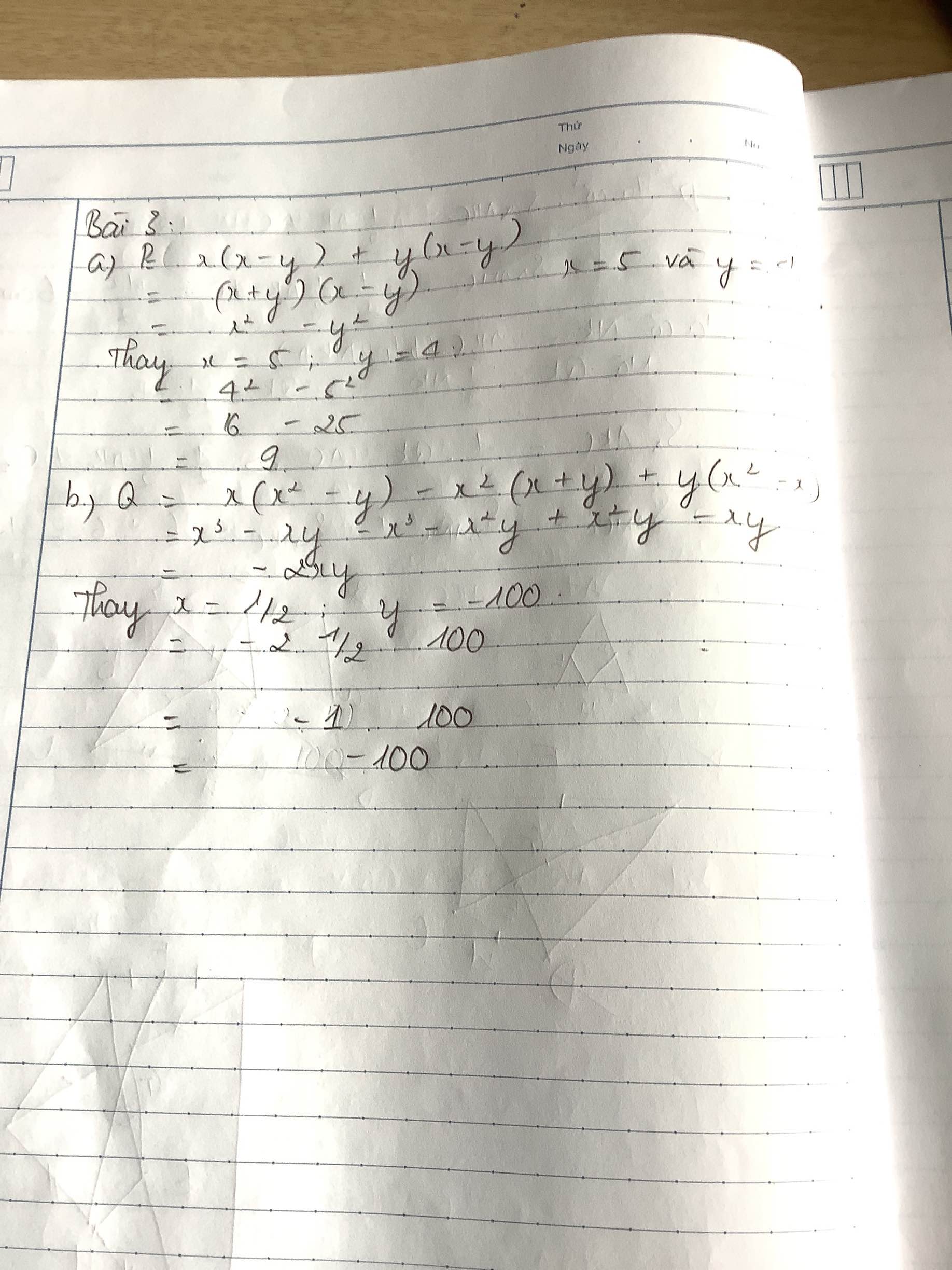Ta có: x ( x - y ) + y ( y - x )  = x(x-y) - y(x-y) =(x-y)^2

Thay x= 53 và y= 3 vào (x-y)^2

Có: (53-3)^2 = 50^2 = 2500

Vậy giá trị biểu thức x ( x - y ) + y ( y - x ) tại x= 53; y= 3 là 2500

biến đổi thành :x(x-y)-y(x-y) rồi dổi thành (x-y)(x-y)=(x-y)^2   rồi thay vào là ra thôi

Ta có: x ( x - y) + y ( y -x ) 

= xx - xy + yy - yx

= xx - yy

= x² - y²

= (x-y)²

Thay vào: (53-3)² = 50² = 2500

a.\(x^2+xy+x=x\left(x+y+1\right)=77\left(77+22+1\right)=77.100=7700\)

b.\(x\left(x-y\right)+y\left(y-x\right)=\left(x-y\right)^2=\left(53-3\right)^2=50^2=2500\)

Đặt A = x² + xy + x 

= x(x + y + 1) 

Thay x = 77 ; y = 22 vào biểu thức ta được 

A = 77(77 + 22 + 1) = 77.100 = 7700

b) Đặt B =  x(x - y) + y(y - x) 

= (x - y)² 

Thay x = 53 ; y = 3 vào biểu thức ta được 

B = (53  - 3)² = 50² = 2500

có ai biết câu này ko:  85.12,7 + 5.3.12,7           

a) \(P=x\left(x-y\right)+y\left(x-y\right)=\left(x-y\right)\left(x+y\right)=x^2-y^2=5^2-4^2=9\)

b) \(Q=x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)=x^3-xy-x^3-x^2y+x^2y-xy=0\)

a: Khi x=2 và y=-3 thì \(x^2+2y=2^2+2\cdot\left(-3\right)=4-6=-2\)

b: \(A=x^2+2xy+y^2=\left(x+y\right)^2\)

Khi x=4 và y=6 thì \(A=\left(4+6\right)^2=10^2=100\)

c: \(P=x^2-4xy+4y^2=\left(x-2y\right)^2\)

Khi x=1 và y=1/2 thì \(P=\left(1-2\cdot\dfrac{1}{2}\right)^2=\left(1-1\right)^2=0\)

a) Thay x = -1 và y = 3 vào A, ta được :

A = 2.(-1)[(-1) + 3] - (-1) + 7 - 3

A = -2.2 + 1 + 4

A = -4 + 5

A = 1

b) |y| = 3 => \(\orbr{\begin{cases}y=3\\y=-3\end{cases}}\)

*Thay x =-1 và y = 3 vào biểu thức :

Phần này bạn sẽ làm ý như câu a vậy :33

*Thay x = -1 và y =-3 vào A, ta được :

A = 2.(-1).[(-1) + (-3)] - (-1) + 7 - (-3)

A = -2.(-4) + 1 + 7 + 3

A = 8 + 11

A = 19

a ) 

Ta có : 

\(x^2+xy+x=x\left(x+y+1\right)\)

Thay \(x=77;y=22\)vào b/t , ta được : 

\(77\left(77+22+1\right)=77.100=7700\)

Vậy \(x^2+xy+x=7700\)tại \(x=77;y=22\)

b ) 

Ta có : 

\(x\left(x-y\right)+y\left(y-x\right)\)

\(=x\left(x-y\right)-y\left(x-y\right)\)

\(=\left(x-y\right)\left(x-y\right)\)

\(=\left(x-y\right)^2\)

Thay \(x=53;y=3\)vào b/t , ta được : 

\(\left(53-3\right)^2=50^2=2500\)

Vậy \(x\left(x-y\right)+y\left(y-x\right)=2500\) tại \(x=53;y=3\)

a) \(x^2+xy+x\)

\(\Leftrightarrow x\left(x+y+1\right)\)

Tại x=77 và y=22 có:

\(\Leftrightarrow77\left(77+22+1\right)\)

\(=7700\)

b) \(x\left(x-y\right)+y\left(y-x\right)\)

\(\Leftrightarrow\left(x-y\right)\left(x+y\right)\)

\(\Leftrightarrow x^2-y^2\)

Tại x=53 và y=3, ta có:

\(53^2-3^2=2800\)

a.

\(x^2+xy+x=x\left(x+y+1\right)\)

Tại \(x=77;y=22\Rightarrow x\left(x+y+1\right)=77\left(77+22+1\right)=77.100=7700\)

b.

\(x\left(x-y\right)+y\left(y-x\right)=x\left(x-y\right)-y\left(x-y\right)=\left(x-y\right)\left(x-y\right)=\left(x-y\right)^2\)

\(=\left(53-3\right)^2=50^2=2500\)

c.

\(x\left(x-1\right)-y\left(1-x\right)=x\left(x-1\right)+y\left(x-1\right)=\left(x+y\right)\left(x-1\right)\)

\(=\left(2001+1999\right)\left(2001-1\right)=4000.2000=8000000\)