Cho tam giác ABC. Gọi M là trung điểm của BC.
a) Chứng minh A M < A B + A C 2
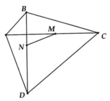
b) Cho bốn điểm A, B, C, D như hình vẽ. Gọi thứ tự là trung điểm của AC và BD. Chứng minh AB + BC + C + DA > 4MN
Cho tam giác ABC vuông tại A, AB = 5cm, AC = 12cm. Gọi E là trung điểm của AC và M là trung điểm của BC.
a) Tính EM .
b) Gọi D là điểm đối xứng với điểm E qua M. Chứng minh: Tứ giác EDBC là hình bình hành
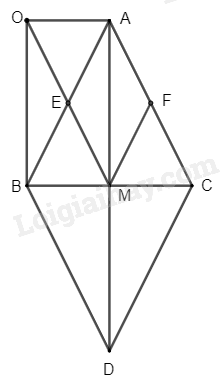
Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
a) Chứng minh tứ giác ABDC là hình thoi
b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh rằng hai tam giác AOB và MBO bằng nhau
c) Chứng minh tứ giác AEMF là hình thoi
a) Xét tứ giác \(ABDC\) có:
\(M\) là trung điểm của \(BC\) (gt)
\(M\) là trung điểm của \(AD\) (do \(D\) đối xứng với \(A\) qua \(BC\))
Suy ra \(ABDC\) là hình bình hành
b) Do \(\Delta ABC\) cân tại \(A\), có \(AM\) là trung tuyến (gt)
Suy ra \(AM\) là đường cao, trung trực, phân giác
Suy ra \(AM\) vuông góc \(BM\) và \(CM\)
Xét tứ giác \(OAMB\) ta có:
\(E\) là trung điểm của \(OM\) và \(AB\) (gt)
Suy ra \(OAMB\) là hình bình hành
Suy ra \(OB\) // \(AM\); \(OA\) // \(MB\); \(OA = BM\); \(OB = AM\)
Mà \(AM \bot BM\) (cmt)
Suy ra: \(AM \bot OA\); \(OB \bot MB\)
Mà \(AM\) // \(OB\) (cmt)
Suy ra \(OB \bot OA\)
Xét \(\Delta AOB\) và \(\Delta MBO\) (các tam giác vuông) ta có:
\(\widehat {{\rm{AOB}}} = \widehat {{\rm{OBM}}} = 90^\circ \)
\(AO = MB\) (cmt)
\(OB = AM\) (cmt)
Suy ra \(\Delta AOB = \Delta MBO\) (c-g-c)
Suy ra \(OM = AB\)
c) \(OM = AB\) (cmt)
Mà \(EM = EO = \frac{1}{2}OM\); \(EA = EB = \frac{1}{2}AB\)
Suy ra \(EO = EA = EM = EB\) (1)
Xét \(\Delta ABC\) cân ta có: \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) và \(AB = AC\)
Mà \(EA = EB = \frac{1}{2}AB\); \(FA = FC = \frac{1}{2}AC\) (gt)
Suy ra \(AE = EB = FA = FM\) (2)
Xét \(\Delta BEM\) và \(\Delta CMF\) ta có:
\(BE = CF\) (cmt)
\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) (cmt)
\(BM = CM\) (gt)
Suy ra \(\Delta BEM = \Delta CFM\) (c-g-c)
Suy ra \(EM = FM\) (3)
Từ (1), (2), (3) suy ra \(AE = AF = FM = ME\)
Suy ra \(AEMF\) là hình thoi
cho tam giác ABC cân tại A. Gọi M, N, H lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh : Tứ giác MNCB là hình thang cân.
b) Gọi D là điểm đối xứng của H qua N. Các tứ giác AHCD, ADNM là hình gì? Vì sao?
c) Chứng minh : N là trọng tâm của tam giác CMD.
d) MD cắt AC tại E. Chứng minh : BN đi qua trung điểm của HE.
cho tam giác ABC cân tại A. Gọi M, N, H lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh : Tứ giác MNCB là hình thang cân.
b) Gọi D là điểm đối xứng của H qua N. Các tứ giác AHCD, ADNM là hình gì? Vì sao?
c) Chứng minh : N là trọng tâm của tam giác CMD.
d) MD cắt AC tại E. Chứng minh : BN đi qua trung điểm của HE.
Giúp câu d ạ
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh ∆ AMB = ∆ AMC.
b) Chứng minh AM là tia phân giác của góc BAC.
c) Chứng minh AM ⊥ BC.
d) Trên nửa mặt phẳng bờ BC không chứa điểm A, lấy điểm D sao cho DB = DC.
Chứng minh ba điểm A, M, D thẳng hàng
Giúp mình vs
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
Cho tam giác ABC vuông tại A. Biết AB = 15 cm, AC = 20 cm. Gọi M, N
lần lượt là trung điểm các cạnh AB, BC.
a) Tính độ dài MN và AN?
b) Gọi D là điểm đối xứng của A qua N. Chứng minh tứ giác ABDC là hình chữ nhật.
c) Gọi E là điểm đối xứng của N qua M. Chứng minh tứ giác ANBE là hình thoi.
a: MN=AC/2=10cm
AN=BC/2=12,5cm
Cho tam giác ABC có A=40°, AB=AC. Gọi M là trung điểm của BC.
a/ chứng minh ABM=ACM
b/ tính B;C
c/ lấy D∈ AB, E∈ AC sao cho AD=AE. Chứng minh DE//BC
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Suy ra: \(\widehat{ABM}=\widehat{ACM}\)
b: Ta có: ΔABC cân tại A
nên \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
c: Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Do đó: DE//BC
Cho tam giác ABC có AB = AC. Gọi H là trung điểm của BC.
a) Chứng minh ΔABH = ΔACH
b) Vẽ HI⊥AB tại I và vẽ HK⊥AC tại K. Chứng minh AI = AK
c) Chứng minh IK // BC
d) Gọi M là trung điểm IK. Chứng minh A, M, H thẳng hàng.
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
DO đó: ΔAHB=ΔAHC
Cho tam giác ABC có AB = AC. Gọi H là trung điểm của BC.
a) Chứng minh tam giác ABH = tam giác ACH
b) Vẽ HI ⊥ AB tại I và vẽ HK ⊥ AC tại K. Chứng minh AI = AK
c) Chứng minh IK // BC d) Gọi M là trung điểm IK. Chứng minh A, M, H thẳng hàng
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
b: Xét ΔAIH vuông tại I và ΔAKH vuông tại K có
AH chung
\(\widehat{IAH}=\widehat{KAH}\)
Do đó: ΔAIH=ΔAKH
Suy ra: AI=AK
c: Xét ΔABC có
AI/AB=AK/AC
nên IK//BC
cho tam giác ABC có AB=AC.Gọi I là trung điểm của BC.
a)Tam giác ABC là tam giác gì?Vì sao?Chứng minh : góc ABC=góc ACB
b)Cho B=70độ.Tính số đo góc C và góc A ?
c)Chứng minh tam giác ABC =tam giác ACI?
d)Trên tia đối của IA lấy điểm M sao cho IM=IA.Chứng minh MB=AC và MB //AC?
e)Gọi K là trung điểm cuả AB.Trên tia đối cuat tia KM lấy điểm N sao cho KM=KN.Chứng minh:A là trung điểm của đoạn thẳng NC
mai thi rồi giúp
a: Xét ΔABC có AB=AC
nên ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
b: Ta có: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
mà \(\widehat{ABC}=70^0\)
nên \(\widehat{ACB}=70^0\)
Ta có: ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{B}=40^0\)
c: Sửa đề: Chứng minh ΔABI=ΔACI
Xét ΔABI và ΔACI có
AB=AC
BI=CI
AI chung
Do đó: ΔABI=ΔACI
d: Xét tứ giác ABMC có
I là trung điểm chung của AM và BC
=>ABMC là hình bình hành
=>MB=AC và MB//AC
e: Xét tứ giác ANBM có
K là trung điểm chung của AB và MN
=>ANBM là hình bình hành
=>AN//BM và AN=BM
Ta có: AN//BM
AC//BM
AN,AC có điểm chung là A
Do đó: N,A,C thẳng hàng
Ta có: AN=BM
AC=BM
Do đó: AN=AC
mà N,A,C thẳng hàng
nên A là trung điểm của NC