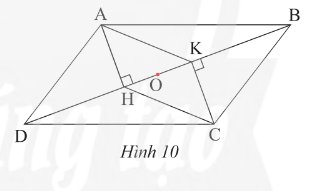
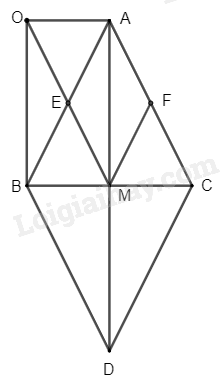
Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
a) Chứng minh tứ giác ABDC là hình thoi
b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh rằng hai tam giác AOB và MBO bằng nhau
c) Chứng minh tứ giác AEMF là hình thoi
a) Xét tứ giác \(ABDC\) có:
\(M\) là trung điểm của \(BC\) (gt)
\(M\) là trung điểm của \(AD\) (do \(D\) đối xứng với \(A\) qua \(BC\))
Suy ra \(ABDC\) là hình bình hành
b) Do \(\Delta ABC\) cân tại \(A\), có \(AM\) là trung tuyến (gt)
Suy ra \(AM\) là đường cao, trung trực, phân giác
Suy ra \(AM\) vuông góc \(BM\) và \(CM\)
Xét tứ giác \(OAMB\) ta có:
\(E\) là trung điểm của \(OM\) và \(AB\) (gt)
Suy ra \(OAMB\) là hình bình hành
Suy ra \(OB\) // \(AM\); \(OA\) // \(MB\); \(OA = BM\); \(OB = AM\)
Mà \(AM \bot BM\) (cmt)
Suy ra: \(AM \bot OA\); \(OB \bot MB\)
Mà \(AM\) // \(OB\) (cmt)
Suy ra \(OB \bot OA\)
Xét \(\Delta AOB\) và \(\Delta MBO\) (các tam giác vuông) ta có:
\(\widehat {{\rm{AOB}}} = \widehat {{\rm{OBM}}} = 90^\circ \)
\(AO = MB\) (cmt)
\(OB = AM\) (cmt)
Suy ra \(\Delta AOB = \Delta MBO\) (c-g-c)
Suy ra \(OM = AB\)
c) \(OM = AB\) (cmt)
Mà \(EM = EO = \frac{1}{2}OM\); \(EA = EB = \frac{1}{2}AB\)
Suy ra \(EO = EA = EM = EB\) (1)
Xét \(\Delta ABC\) cân ta có: \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) và \(AB = AC\)
Mà \(EA = EB = \frac{1}{2}AB\); \(FA = FC = \frac{1}{2}AC\) (gt)
Suy ra \(AE = EB = FA = FM\) (2)
Xét \(\Delta BEM\) và \(\Delta CMF\) ta có:
\(BE = CF\) (cmt)
\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) (cmt)
\(BM = CM\) (gt)
Suy ra \(\Delta BEM = \Delta CFM\) (c-g-c)
Suy ra \(EM = FM\) (3)
Từ (1), (2), (3) suy ra \(AE = AF = FM = ME\)
Suy ra \(AEMF\) là hình thoi