Biết rằng phương trình 2 - x + 2 + x - 4 - x 2 = m có nghiệm khi m thuộc [a;b] với a,b ∈ ℝ . Khi đó giá trị của T = ( a + 2 ) 2 + b là?
A. T = 3 2 + 2
B. T = 6
C. T = 8
D. T = 0
Cho 2 phương trình x^2 + 2015x - 2016 = 0 và y^2 + 2015y - 2016 = 0.
Không giải phương trình có cách nào tính được x - y, x + y hay không? Biết rằng x > y.
Nhìn là biết đáp án x-y=0 và x+y=2 mà bạn. Do x=1, y=1
Biết rằng phương trình \(\left(m-3\right)x^2-2\left(m+1\right)x-m-3=0\)
có một nghiệm là −1, nghiệm còn lại
của phương trình là:
Phương trình có một nghiệm là -1.
\(\Rightarrow-2\left(m+1\right)=m-3-m-3\)
\(\Leftrightarrow m=2\)
Phương trình trở thành:
\(-x^2-6x-5=0\)
\(\Leftrightarrow-\left(x+1\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=-1\\x_2=-5\end{matrix}\right.\)
Vậy nghiệm còn lại là \(x_2=-5\).
Cho phương trình x2+bx+c=0 (*) với b,c là các số thõa mãn 2b+4c=-1
a. chứng tỏ rằng phương trình (*) luôn có nghiệm
b. Tìm b,c biết rằng phương trình (*) có 2 nghiệm x1,x2 với x1-2x2=0
a) đenta=b^2-4c
2b+4c=-1=>c=-1-2b)/4
thay vô chứng minh nó lớn hơn 0
x1+x2=b
x1x2=c
ta có x1=2x2
thay vô tìm x1;x2 theo b,c rồi thay vô
mk tính được x1=2x;x2=b/3 thay cái này vô x1-2x2=0 tìm ra b
x1=căn(c/2);x2=căn(2c) thay vô cái x1-2x2=0 tìm ra c
Giải phương trình x2 - mx + n = 0 biết rằng phương trình có hai nghiệm x1, x2 là các số nguyên và m, n là các số nguyên tố
Lời giải:
Để PT có nghiệm nguyên thì:
$\Delta=m^2-4n=a^2$ với $a$ là số tự nhiên.
$\Rightarrow 4n=(m-a)(m+a)$
Vì $n$ là số nguyên tố nên và $m-a< m+a$ với $a$ tự nhiên, $m+a, m-a$ cùng tính chẵn lẻ nên ta xét các TH sau đây:
TH1:
$m-a=2, m+a=2n\Rightarrow m=n+1$
$\Rightarrow m,n$ khác tính chẵn lẻ. Mà $m,n$ nguyên tố nên 1 trong 2 số bằng 2.
$n< m$ nên $n=2\Rightarrow m=3$.
TH2:
$m-a=4, m+a=n$
Vì $m-a$ chẵn nên $m+a$ chẵn. Hay $n$ chẵn $\Rightarrow n=2$
$\Rightarrow m+a< m-a$ (vô lý - loại)
Vậy........
Lời giải:
Để PT có nghiệm nguyên thì:
$\Delta=m^2-4n=a^2$ với $a$ là số tự nhiên.
$\Rightarrow 4n=(m-a)(m+a)$
Vì $n$ là số nguyên tố nên và $m-a< m+a$ với $a$ tự nhiên, $m+a, m-a$ cùng tính chẵn lẻ nên ta xét các TH sau đây:
TH1:
$m-a=2, m+a=2n\Rightarrow m=n+1$
$\Rightarrow m,n$ khác tính chẵn lẻ. Mà $m,n$ nguyên tố nên 1 trong 2 số bằng 2.
$n< m$ nên $n=2\Rightarrow m=3$.
TH2:
$m-a=4, m+a=n$
Vì $m-a$ chẵn nên $m+a$ chẵn. Hay $n$ chẵn $\Rightarrow n=2$
$\Rightarrow m+a< m-a$ (vô lý - loại)
Vậy........
Giải phương trình:
x4 - 6x3-x2+54x-72=0
Biết rằng phương trình có một nghiệm là x=1
Phương trình này không có nghiệm là x = 1 nha bạn
Biết rằng phương trình x - 2 log 2 4 x - 2 = 4 . x - 2 3 có hai nghiệm x 1 , x 2 x 1 < x 2 . Tính 2 x 1 - x 2 .
A. 1
B. 3
C. -5
D. -1
Đáp án D.
ĐK: x > 2.
TH1: Ta thấy x = 3 không phải là nghiệm của PT.
TH2: Với x ≠ 3 logarit cơ số x - 2 cả 2 vế ta được log 2 4 x - 2 = log x - 2 4 + 3
⇔ 2 + log 2 x - 2 = 2 log x - 2 2 + 3 ⇔ log 2 x - 2 - 2 log x - 2 2 - 1 = 0
Đặt t = log 2 x - 2 ⇒ t - 2 t - 1 = 0 ⇔ t 2 - t - 2 = 0 ⇔ [ t = - 1 t = 2
Với t = - 1 ⇒ x = 5 2 ; với t = 2 ⇒ x = 6 ⇒ [ x 1 = 5 2 x 2 = 6 ⇒ 2 x 1 - x 2 = - 1 .
giải phương trình: 2x= 7 -5/x
tìm 2 số x, y biết rằng x + y= 3 và xy=1
\(2x=7-\dfrac{5}{x}\)đk x khác 0
\(2x^2-7x+5=0\Leftrightarrow\left(x-1\right)\left(2x-5\right)=0\Leftrightarrow x=1;x=\dfrac{5}{2}\left(tm\right)\)
Cho phương trình: x\(^2\) + 2(m+2)x - (4m+12) = 0
a)Chứng minh rằng phương trình luôn có nghiệm với mọi m
b)Xác định m để phương trình có 2 nghiệm x\(_1\), x\(_2\) thoả mãn x\(_1\)=x\(_2\)\(^2\)
a,Có \(\Delta=4\left(m+2\right)^2-4.-\left(4m+12\right)=4m^2+32m+64=4\left(m+4\right)^2\ge0\forall m\)
=> Phương trình luôn có nghiệm với mọi m
b,Phương trình có nghiệm \(\left[{}\begin{matrix}x=\dfrac{-2\left(m+2\right)+2\left(m+4\right)}{2}=2\\x=\dfrac{-2\left(m+2\right)-2\left(m+4\right)}{2}=-2m-6\end{matrix}\right.\) (ở đây không cần chia trường hợp của m bởi khi chia trường hợp thì x chỉ đổi giá trị cho nhau)
TH1: \(x_1=x_2^2\Leftrightarrow4=\left(-2m-6\right)^2\)\(\Leftrightarrow\left[{}\begin{matrix}m=-2\\m=-4\end{matrix}\right.\) (Thay vào pt thấy không thỏa mãn)
TH2:\(x_1=x_2^2\Leftrightarrow-2m-6=2^2\)\(\Leftrightarrow m=-5\) (Thay vào pt thấy thỏa mãn)
Vậy ...
Biết rằng phương trình x - 2 log 2 4 x - 2 = 4 . x - 2 3 có hai nghiệm x1, x2 (x1 < x2). Tính 2x1 – x2.
A. 1.
B. 3.
C. -5.
D. -1.
Đáp án D.
ĐK: x > 2.
TH1: Ta thấy x = 3 không phải là nghiệm của PT.
TH2: Với x ≠ 3 logarit cơ số x – 2 cả 2 vế ta được
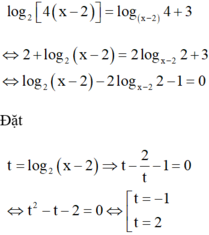
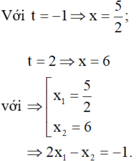
biết rằng phương trình \(x^2+px+1=0\) có nghiệm là a,b và phương trình \(x^2+qx+2=0\) có nghiêm là b,c . Khi đó giá trị của biểu thức \(A=pq-\left(b-a\right)\left(b-c\right)\)bằng ?
Áp dụng viet vào pt \(x^2+px+1=0\) ta được:\(\left\{{}\begin{matrix}a+b=-p\\ab=1\end{matrix}\right.\)
Áp dụng viet vào pt \(x^2+qx+2=0\) ta được:\(\left\{{}\begin{matrix}b+c=-q\\bc=2\end{matrix}\right.\)
\(A=pq-\left(b-a\right)\left(b-c\right)=-\left(a+b\right).-\left(b+c\right)-\left(b^2-bc-ab+ac\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
\(=2ab+2bc=6\)
Phương trình: \(x^2+px+1=0\)
Có 2 nghiệm:a,b
\(\Rightarrow\left\{{}\begin{matrix}a+b=-p\\a.b=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}p=-\left(a+b\right)\\1=a.b\end{matrix}\right.\)
Phương trình \(x^2+px+2=0\)
Có 2 nghiệm:b,c
\(\Rightarrow\left\{{}\begin{matrix}b+c=-q\\b.c=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}q=-\left(b+c\right)\\2=b.c\end{matrix}\right.\)
Ta có: \(p.q-\left(b-a\right)\left(b-c\right)\)
\(=-\left(a+b\right).\left[-\left(b+c\right)\right]-\left(b-a\right)\left(b-c\right)\)
\(=\left(a+b\right)\left(b+c\right)-\left(b-a\right)\left(b-c\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
=\(\left(ab+ab\right)+\left(ac-ac\right)+\left(b^2-b^2\right)+\left(bc+bc\right)\)
\(=2ab+2bc\)
\(=2.1+2.2\)
=6
-Chúc bạn học tốt-