Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc A B C ^ = 60 0 . Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB.
A . S = 25 π 3 3 c m 2
B . S = 25 π c m 2
C . S = 25 π 3 4 c m 2
D . S = 25 π 3 c m 2
Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc A B C ^ = 60 ° . Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB.
A. S = 25 π 3 3 c m 2
B. S = 25 π c m 2
C. S = 25 π 3 4 c m 2
D. S = 25 π 3 c m 2
Trong không gian cho hình thoi ABCD có cạnh là 5cm và góc A B C ⏜ = 60 ° . Tính diện tích xung quanh S của hình thu được khi quay hình thoi quanh trục DB.
A. S = 25 π 3 3 c m 2
B. S = 25 π c m 2
C. S = 25 π 3 4 c m 2
D. S = 25 π 3 cm 2
Đáp án B.
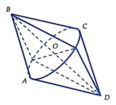
Do A B C ⏜ = 60 ° đều ⇒ A C = 5 c m cm
Do đó diện tích của hình thu được: S = 2 π . AC 2 . BA = 25 π cm 2 cm2
Cho hình thoi ABCD có cạnh là 5cm, đường cao là 2,5cm và A>B . Số đo các góc của hình thoi là
MN giúp mình với
Cho hình chóp S ABCD . có đáy ABCD là hình thoi cạnh 2a, SA a = 5 ; góc BCD = 60 o và SA vuông góc với ( ) ABCD . Gọi K là trung điểm của CD. Tính góc giữa đường thẳng SK và ( SAB ).
A. 450 . B. 300 . C. 600 . D. arctan \(\dfrac{\sqrt{7}}{\sqrt{5}}\)
help me
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ABC = 60 ° cạnh bên SA = a 2 và SA vuông góc với ABCD. Tính góc giữa SB và (SAC).
A. 90 °
B. 30 °
C. 45 °
D. 60 °
Chọn B.
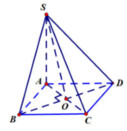
Gọi O = AC ∩ BD. Vì ABCD là hình thoi nên BO ⊥ AC(1). Lại do:
![]()
Từ (1) và (2) ta có:BO ⊥ (SAC)
![]()
Ta có: ![]()
Vì ABCD là hình thoi có ABC = 60 ° nên tam giác ABC đều cạnh a
![]()
Trong tam giác vuông SBO ta có:
Đề thiếu dữ liệu để xác định độ dài SA rồi bạn
Cho hình chóp SABCD. ABCD là hình thoi tâm Ở cạnh a. Góc BAD=60°. SO vuông góc với (ABCD). Góc giữa SC và đáy bằng 60°. Tính khoảng cách a)O đến (SBC) b)A đến (SBC) c)AD đến (SCD)
cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, SA vuông góc với mặt phẳng đáy, SA=BD=a√3. Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) bằng
A. 60° B. 30° C.90° D.45°
Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc B A D ⏜ có số đo bằng 60 ° . Hình chiếu của S lên mặt phẳng (ABCD) là trọng tâm tam giác ABC .Góc giữa (ABCD) và (SAB) bằng 60 ° . Tính khoảng cách từ B đến mặt phẳng (SCD) .
A. 3 a 17 14
B. 3 a 7 14
C. 3 a 17 4
D. 3 7 4
Đáp án B
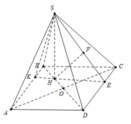
Gọi H là trọng tâm Δ A B C
Dựng H K ⊥ A B , H E ⊥ C D , H F ⊥ S E
Ta có A B ⊥ S H K ⇒ S K H ⏜ = 60 °
Do đó S H = H K tan 60 °
Mặc khác H K = H B sin 60 ° ( Do Δ A B C là tam giác đều nên A B D ⏜ = 60 ° ) suy ra H K = a 3 sin 60 ° = a 3 6 ⇒ S H = a 2
Lại có H E = H D tan 60 ° = a 3 3 ⇒ H F = a 7 = d H ; S C D
Do đó B D H D = 3 2 ⇒ d B = 3 2 d H = 3 a 17 14