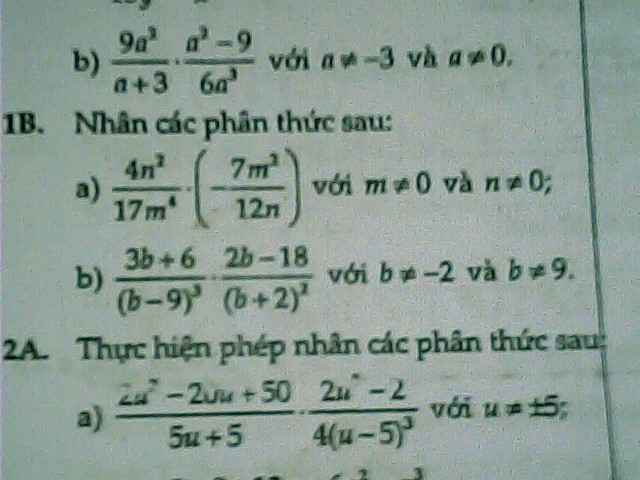
Em cần 1b thôi ạ
TK
Những câu hỏi liên quan
em chỉ cần bài văng bình thường thôi ạ không cần dài quá đâu ạ em cảm ơn
Giúp em với. Em đang cần gấp ạ,( làm giúp em bài 3 thôi ạ.
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
Giúp mik bài này vs ạ, chỉ cần cậ d thôi ạ( mn giúp em vs em đang cần gấp )
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
Đúng 0
Bình luận (0)
NT
27 tháng 3 2022 lúc 11:14
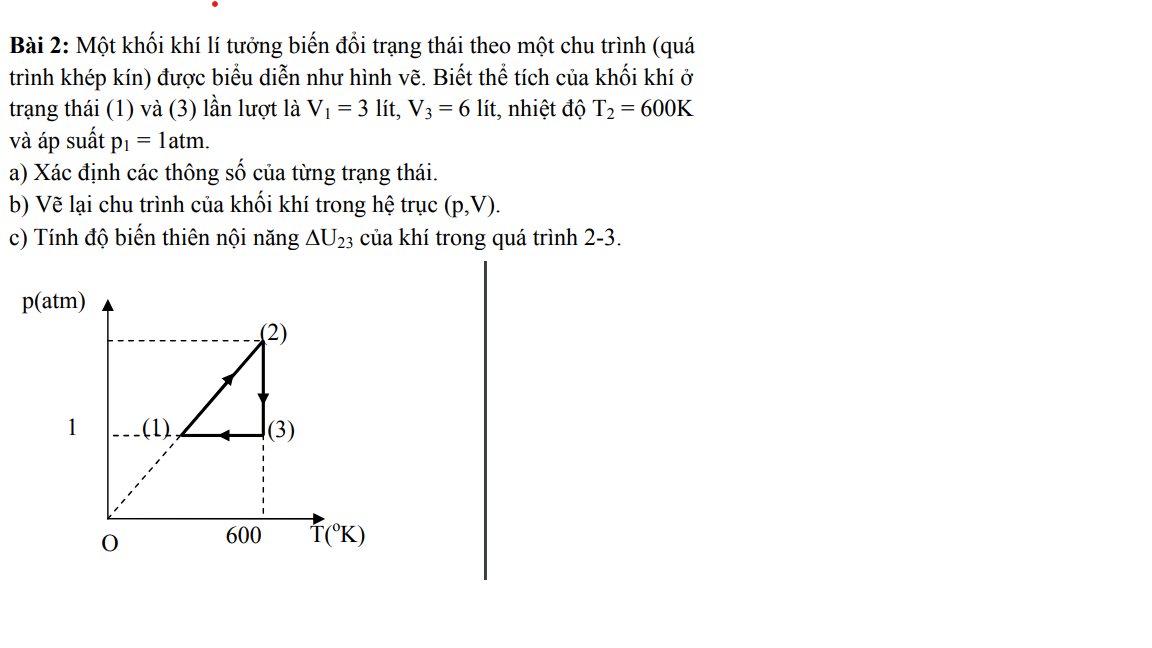
Dạ em chỉ cần câu c thôi ạ, mọi người giúp em với ạ
cho hệ phương trình
mx + y= 5
2x - y= -2
a)giải hệ phương trình khi m=1
b)xác định giá trị của m để nghiệm (xo,yo) của hệ phương trình thỏa mãn điều kiện xo+yo=1
giúp em câu B thôi ạ
Cho em hỏi:
A(x) = 6x3 - x - 1
B(x) = 5x3 - 2x + x2 - 1
a) Tính: P(x) = A(x) + B(x).
b) Tính: Q(x) = A(x) - B(x).
c) Tính U(x) biết 2U(x) + 3A(x) = B(x).
Nhiêu đó thôi ạ!
a: \(P\left(x\right)=6x^3-x-1+5x^3+x^2-2x-1=11x^3+x^2-3x-2\)
b: \(Q\left(x\right)=6x^3-x-1-5x^3-x^2+2x+1=x^3-x^2+x\)
c: \(2\cdot U\left(x\right)=5x^3-2x+x^2-1-3\cdot\left(6x^3-x-1\right)\)
\(\Leftrightarrow2\cdot U\left(x\right)=5x^3+x^2-2x-1-18x^3+3x+3\)
\(\Leftrightarrow2\cdot U\left(x\right)=-13x^3+x^2+x+2\)
hay \(U\left(x\right)=-\dfrac{13}{2}x^3+\dfrac{1}{2}x^2+\dfrac{1}{2}x+1\)
Đúng 3
Bình luận (0)
\(a,P\left(x\right)=A\left(x\right)+B\left(x\right)=6x^3-x-1+5x^3-2x+x^2-1=11x^3+x^2+x-2\)
\(b,Q\left(x\right)=A\left(x\right)-B\left(x\right)=6x^3-x-1-5x^3+2x-x^2+1=x^3-x^2+x\)
c, Ta có : \(2U\left(x\right)+2A\left(x\right)=B\left(x\right)\)
hay \(2U\left(x\right)+2\left(6x^3-x-1\right)=5x^3-2x+x^2-1\)
\(\Rightarrow2U\left(x\right)+12x^3-2x-2=5x^3-2x+x^2-1\)
\(\Rightarrow2U\left(x\right)=5x^3-2x+x^2-1-12x^3+2x+2\)
\(\Rightarrow U\left(x\right)=-7x^3+x^2+1\)
Đúng 1
Bình luận (0)
VN
16 tháng 10 2021 lúc 21:13
Em đang cần gấp ạ có 1 bài thôi ạ
mọi người ơi giúp em câu b thôi ạ
cần gấp ạ em cảm ơn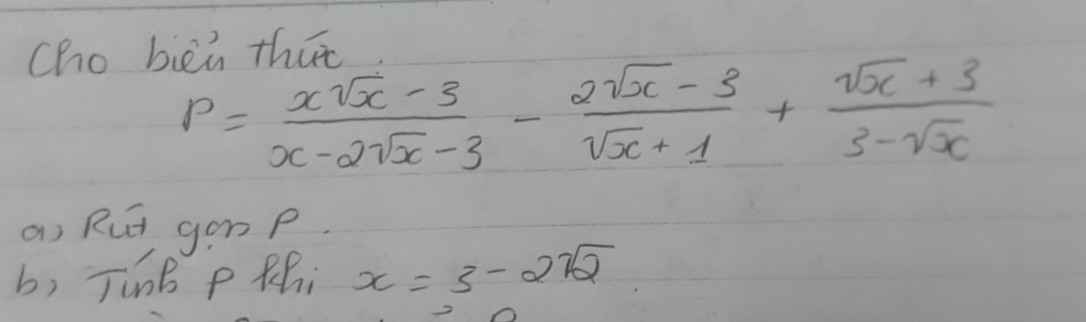
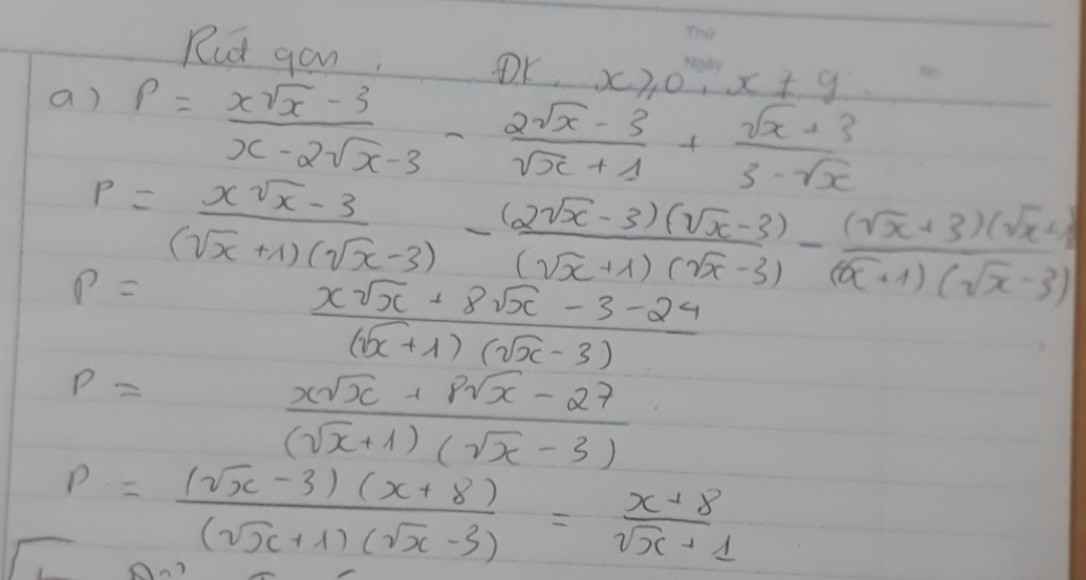
thay \(x=3-2\sqrt{2}\) vào P ta có:
\(\dfrac{x+8}{\sqrt{x}+1}=\dfrac{3-2\sqrt{2}+8}{\sqrt{3-2\sqrt{2}}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}-1+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}}\)
Đúng 2
Bình luận (0)
\(b,x=3-2\sqrt{2}=\left(\sqrt{2}-1\right)^2\)
Thay vào P, ta được:
\(P=\dfrac{3-2\sqrt{2}+8}{\sqrt{\left(\sqrt{2}-1\right)^2}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}}=\dfrac{11\sqrt{2}-4}{2}\)
Đúng 3
Bình luận (0)
b: Thay \(x=3+2\sqrt{2}\) vào P, ta được:
\(P=\dfrac{3+2\sqrt{2}+8}{2+\sqrt{2}}=\dfrac{18-7\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)