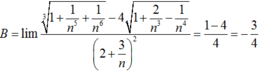Giới hạn của dãy số ( u n ) với u n = 3 n 3 + 2 n - 1 2 n 2 - n , bằng
A. 3 2
B. 0
C. + ∞
D. 1
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Câu 1:
Dãy số (un) với un=\(\dfrac{2^n-5.7^{n+1}}{2^n+7^n}\) có giới hạn bằng:
A, 15
B, -25
C, -35
D, Một kết quả khác
Câu 2:
Dãy số (un) với un=\(\dfrac{3^n-2.5^{n+1}}{2^n+7^n}\) có giới hạn bằng:
A, -10
B, -5
C, 15
D, Một kết quả khác
Câu 3:
Dãy số (un) với un= \(\sqrt[3]{\dfrac{5-8n}{n+3}}\) có giới hạn bằng:
A, -1
B, -2
C, 2
D, -8
1/ \(\lim\limits\dfrac{\dfrac{2^n}{7^n}-5.7.\left(\dfrac{7}{7}\right)^n}{\dfrac{2^n}{7^n}+\left(\dfrac{7}{7}\right)^n}=-35\)
2/ \(\lim\limits\dfrac{\dfrac{3^n}{7^n}-2.5.\left(\dfrac{5}{7}\right)^n}{\dfrac{2^n}{7^n}+\dfrac{7^n}{7^n}}=0\)
3/ \(\lim\limits\sqrt[3]{\dfrac{\dfrac{5}{n}-\dfrac{8n}{n}}{\dfrac{n}{n}+\dfrac{3}{n}}}=\sqrt[3]{-8}=-2\)
Cho dãy số:
\(u:{\mathbb{N}^*} \to \mathbb{R}\)
\(n \mapsto {u_n} = {n^3}\)
a) Hãy cho biết dãy số trên là hữu hạn hay vô hạn.
b) Viết năm số hạng đầu tiên của dãy số đã cho.
a) Vì hàm số \(u\) xác định trên tập hợp các số nguyên dương
\(\mathbb{N}^{\text{∗
}}\) nên nó là một dãy số vô hạn.
b) Ta có:
\(u_1=1^3=1\\ u_2=2^3=8\\ u_3=3^3=27\\ u_4=4^3=64\\ u_5=5^3=125.\)
a: Dáy số này là vô hạng
b: 1;8;27;64;125
Tính giới hạn của dãy số \(u_n=q+2q^2+3q^3+...+nq^n\) với \(\left|q\right|< 1\)
Nếu ở hệ số ở mũ 2 là 1 có khi xài đạo hàm chút là ra tổng quát, còn cái này thì...khó :D
Gọi q là k đi, máy tui kẹt chữ q, xài On-screen keyboard mệt lắm
\(u_n=k+2k^2+3k^3+...+nk^n\)
Nhận thấy nếu giờ chia k cho un thì sẽ có \(1+2k+3k+...+nk^{n-1}\), ta đã đưa về dạng tổng quát có thể đạo hàm được, sau đó chỉ cần nhân k là ra un
\(\dfrac{u_n}{k}=1+2k+3k^2+...+nk^{n-1}\)
\(f\left(x\right)=1+k+k^2+...+k^n\)
\(\left\{{}\begin{matrix}u_1=1\\q=k\end{matrix}\right.\Rightarrow f\left(x\right)=1.\dfrac{q^{n+1}-1}{q-1}=\dfrac{k^{n+1}-1}{k-1}\)
Dao ham 2 ve:
\(\Rightarrow f'\left(x\right)=1+2k+3k^2+...+nk^{n-1}=\dfrac{\left(k^{n+1}-1\right)'\left(k-1\right)-\left(k-1\right)'\left(k^{n+1}-1\right)}{\left(k-1\right)^2}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{\left(n+1\right)k^n\left(k-1\right)-k^{n+1}+1}{\left(k-1\right)^2}\)
\(f'\left(x\right)=\dfrac{k^n\left[\left(n+1\right)\left(k-1\right)-k\right]+1}{\left(k-1\right)^2}\)
\(\Rightarrow f'\left(x\right)=\dfrac{u_n}{k}\Rightarrow u_n=f'\left(x\right).k=\dfrac{k^{n+1}\left[\left(n+1\right)\left(k-1\right)-k\right]+k}{\left(k-1\right)^2}\)
\(\Rightarrow lim\left(u_n\right)=lim\dfrac{k^{n+1}\left[\left(n+1\right)\left(k-1\right)-k\right]+k}{\left(k-1\right)^2}=\lim\limits\dfrac{k^{n+1}\left[\left(n+1\right)\left(k-1\right)-k\right]}{\left(k-1\right)^2}+\dfrac{k}{\left(k-1\right)^2}\)
\(\left|k\right|< 1\Rightarrow lim\left(k^{n+1}\right)=0\)
\(\Rightarrow\lim\limits\left(u_n\right)=\dfrac{k}{\left(k-1\right)^2}\)
P/s: Một cách làm rất mới mẻ, có thể tổng quát cho nhiều bài toàn sinh ra từ dãy số vừa rồi :D
Lời giải:
\(u_n=q+2q^2+3q^3+...+nq^n\)
\(qu_n=q^2+2q^3+3a^4+...+nq^{n+1}\)
\(\Rightarrow u_n(1-q)=q+q^2+q^3+...+q^n-nq^{n+1}\)
\(\Leftrightarrow u_n(1-q)=q.\frac{q^n-1}{q-1}-nq^{n+1}\)
\(\Leftrightarrow u_n=q.\frac{1-q^n}{(1-q)^2}+\frac{nq^{n+1}}{q-1}=\frac{q-q^{n+1}}{(1-q)^2}+\frac{nq^{n+1}}{q-1}\)
Vì $|q|< 1$ nên $\lim\limits q^{n+1}=0$ nên $\lim\limits u_n=\frac{q}{(1-q)^2}$
Cho dãy số (Un) xác định bởi: { U1=1; Un+1=1/2un + 3/2; ∀n ϵ N*
Tình giới hạn của dãy số (Un)
Ai đó giúp em với, em cảm ơn rất nhiều ạ
1) So sánh quần cư nông thôn và quần cư thành thị. Nêu tình hình đô thị hóa trên thế giới.
2) Nêu giới hạn và đặc điểm đới nóng.
3) Nêu giới hạn và đặc điểm của môi trường xích đạo ẩm.
4) Nêu giới hạn và đặc điểm của môi trường nhiệt đới.
5) Nêu giới hạn, khí hậu và đặc điểm của môi trường nhiệt đới gió mùa.
1)
Quần cư nông thôn:
Có mật độ dân số thấp. Sống theo làng mạc, thôn xóm. Chủ yếu là nhà sàn gắn liền với ruộng nương. Sống theo quản hệ thị tộc (dòng máu). Nghề chủ yếu là sản xuất nông, lâm ngư nghiệp.
Quần cư đô thị:
2.
- Vị trí: nằm ở giữa 2 đường chí tuyến
- Đặc điểm: + là khu vực nhận được nhiều ánh sáng từ mặt trời
+ Nhiệt độ trung bình luôn trên 20oC
+ Có gió tín phong thổi quanh năm
+ Lượng mưa trung bình từ 1000mm đến 2000mm một năm
+ Sinh vật phong phú và đa dạng
+ Dân cư tập trung đông đúc
3.
- Vị trí : \(5^0B->5^0N\)
* Đặc điểm
-Khí hậu
+Nhiệt độ khoảng từ 25 độ C đến 30 độ C.
+Lượng mưa trung bình một năm từ 1500mm đến 2500mm, mưa quanh năm.
+Độ ẩm cao , trung bình trên 80%, nên không khí ẩm ướt , ngột ngạt.
+Thời tiết nóng ẩm quanh năm.
Cho dãy số thực (un) xác định bởi \(\left\{{}\begin{matrix}u_1=2019\\u^2_n+2018u_n-2020u_{n+1}+1=0\left(n\in N\cdot\right)\end{matrix}\right.\). Tìm giới hạn của dãy số (Sn), biết: Sn = \(\dfrac{1}{u_1+2019}+\dfrac{1}{u_2+2019}+...+\dfrac{1}{u_n+2019}\)
Đề không cho sẵn dãy tăng à? Vậy phải chứng minh nó tăng trước
\(u_{n+1}=\dfrac{u_n^2+2018u_n+1}{2020}\)
\(u_{n+1}-u_n=\dfrac{u_n^2+2018u_n+1}{2020}-u_n=\dfrac{\left(u_n-1\right)^2}{2020}\ge0\) \(\Rightarrow\) dãy tăng và không bị chặn trên \(\Rightarrow lim\left(u_n\right)=+\infty\)
\(\Rightarrow2020u_{n+1}=u_n^2+2018u_n+1\)
\(\Leftrightarrow2020u_{n+1}-2020=u_n^2+2018u_n-2019\)
\(\Leftrightarrow2020\left(u_{n+1}-1\right)=\left(u_n+2019\right)\left(u_n-1\right)\)
\(\Rightarrow\dfrac{1}{2020\left(u_{n+1}-1\right)}=\dfrac{1}{\left(u_n+2019\right)\left(u_n-1\right)}=\dfrac{1}{2020}\left(\dfrac{1}{u_n-1}-\dfrac{1}{u_n+2019}\right)\)
\(\Rightarrow\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Thế n=1;2;...;n ta được:
\(\dfrac{1}{u_1+2019}=\dfrac{1}{u_1-1}-\dfrac{1}{u_2-1}\)
\(\dfrac{1}{u_2+2019}=\dfrac{1}{u_2-1}-\dfrac{1}{u_3-1}\)
...
\(\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Cộng vế: \(S_n=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}=\dfrac{1}{2018}-\dfrac{1}{u_{n+1}-1}\)
\(\Rightarrow\lim\left(S_n\right)=\dfrac{1}{2018}-\dfrac{1}{\infty}=\dfrac{1}{2018}\)
Cho dãy số (Un) được xác định như sau: \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\). Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó
Cho dãy số (Un) được xác định như sau \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\) . Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó
a,CMR :dãy u(n)=\(\left(1+\dfrac{1}{n}\right)^n\)có giới hạ hữu hạn
b đặt lim(1+\(\dfrac{1}{n}\))^n =e .Tính các giưới hạn sau ; lim\(\left(\dfrac{n+1}{n-1}\right)^{n+2}\)và lim\(\left(\dfrac{n-2}{n+3}\right)^{n+1}\)
Tính giới hạn của dãy số B = l i m n 6 + n + 1 3 - 4 n 4 + 2 n - 1 ( 2 n + 3 ) 2
A. +∞
B. -∞
C. 3
D. -3/4
Chọn D.
Chia cả tử và mẫu cho n2 ta có được: