Biết nghiệm của hệ phương trình 1 x − 1 y = 1 3 x + 4 y = 5 là (x; y). Tính 9x + 2y
A. 10
B. 14
C. 11
D. 13
Cho hệ phương trình x + 1 y = 2 2 x − 3 y = 1 . Biết nghiệm của hệ phương trình là (x; y), tính 5 x y
A. 35 3
B. 21 5
C. 7 3
D. 21 25
ĐK: y ≠ 0
Ta có
x + 1 y = 2 2 x − 3 y = 1 ⇔ 2 x + 2 y = 4 2 x − 3 y = 1 ⇔ x + 1 y = 2 5 y = 3 ⇔ y = 5 3 x + 1 5 3 = 2 ⇔ x = 7 5 y = 5 3
Vậy hệ phương trình có 1 nghiệm duy nhất ( x ; y ) = 7 5 ; 5 3 ⇒ 5 x y = 21 5
Đáp án: B
Bài tập 1 Cho hệ phương trình  (1)
(1)
1. Giải hệ phương trình (1) khi m = 3 .
2. Tìm m để hệ phương trình có nghiệm x = ![]() và y =
và y = ![]() .
.
3. Tìm nghiệm của hệ phương trình (1) theo m.
Không giải hệ phương trình, hãy cho biết số nghiệm của mỗi hệ phương trình sau:
a) \(\left\{{}\begin{matrix}2x-y=1\\x-2y=-1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2x-y=1\\x-2y=-1\end{matrix}\right.\)
Ta có:
\(D=-4+1=-3\ne0\)
\(D_x=-2-1=-3\ne0\)
\(D_y=-2-1=-3\ne0\)
Vậy Hệ phương trình đã cho có 1 nghiệm duy nhất.
Không giải hệ phương trình, hãy cho biết số nghiệm của mỗi hệ phương trình sau:
b) \(\left\{{}\begin{matrix}2x+y=4\\-x+y=1\end{matrix}\right.\)
Ta có:
2/(-1) ≠ 1/1 (-2 ≠ 1)
⇒ Hệ phương trình đã cho có nghiệm duy nhất
Cho hệ phương trình x + 0 y = - 2 5 x - y = - 9
Nghiệm của hệ phương trình này có phải là nghiệm của phương trình 3x – 7y = 1 hay không?
Thay x = -2, y = -1 vào phương trình 3x – 7y = 1, ta có:
3.(-2) – 7.(-1) = -6 + 7 = 1
Vậy x và y thỏa phương trình 3x – 7y = 1 nên (x; y) = (-2; -1) là nghiệm của phương trình 3x – 7y = 1.
cho hệ phương trình
x + y = m
2x - my = 0
1, giải hệ phương trình (1) khi m=-1
2, xác định giá trí của m để
a, x=1 và y=1 là nghiệm của hệ (1)
b, hệ (1) vô nghiệm
3, tìm nghiệm của hệ phương trinh (1) theo m
4, tìm m để hệ (1) có nghiệm (x,y) thỏa: x + y =1
Cho hệ phương trình x + my =2m hoặc mx + y = 1-m (m là tham số )
1.Tìm các giá trị của m để hệ phương trình :
a)Có nghiệm duy nhất. Tìm nghiệm duy nhất đó
b)Vô nghiệm
c)Vô số nghiệm
2.Trong trường hợp hệ phương trình có nghiệm duy nhất (x,y)
a)Hãy tìm giá trị m nguyên để x và y cùng nguyên
b)tìm hệ thức liên hệ giữa x và y không phụ thuộc m
Biết (x; y) là 1 nghiệm của hệ phương trình: - 5 x + 2 y = 20 3 x + 4 y = - 25 . Khi đó:
A. x = 2y
B. x = -y
C. x = 3y
D. x = 4y
Trong các khẳng định sau, khẳng định nào đúng?
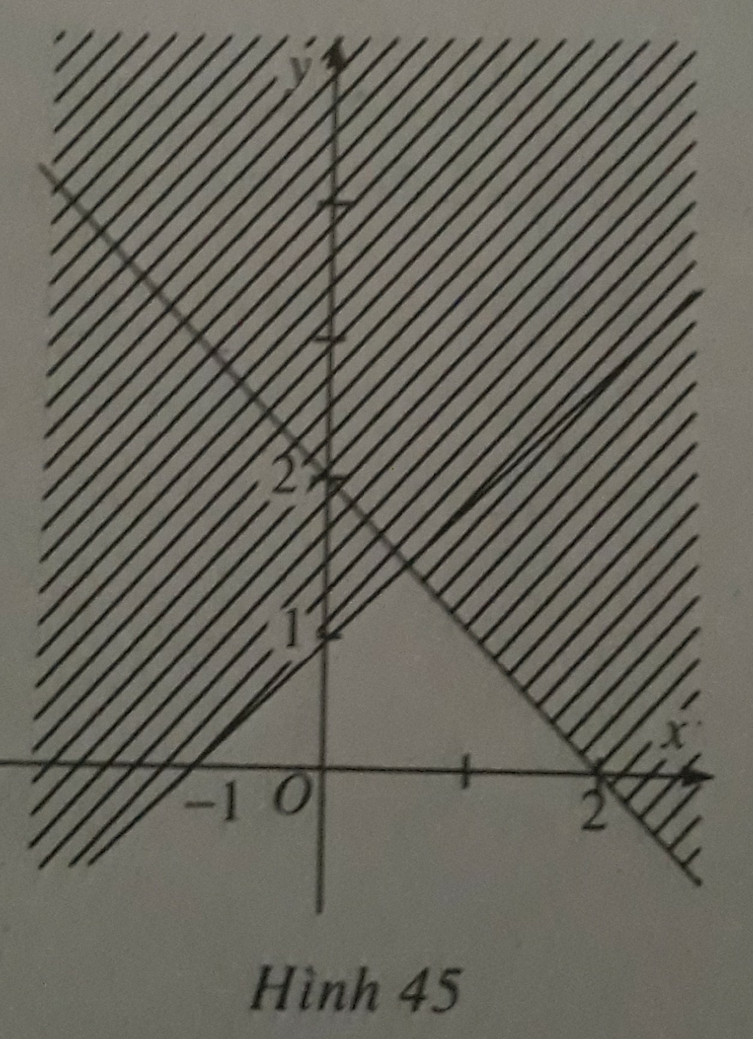
A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2.
B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình![]()
và (x; y) = (-1; 1) là một nghiệm của hệ.
C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình ![]() và (x; y) = (-2; 1) là một nghiệm của hệ.
và (x; y) = (-2; 1) là một nghiệm của hệ.
D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình 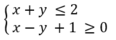 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.
Cho hệ phương trình: \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)
a/Với giá trị nào của k thì hệ phương trình có nghiệm là \(\left(x;y\right)=\left(2;-1\right)\)
b/Với giá trị nào của k thì hệ phương trình có nghiệm duy nhất?hệ phương trình vô nghiệm?
a) Ta có hệ phương trình \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\) Thay nghiệm \(\left(x,y\right)=\left(2,-1\right)\) ta có hệ mới là :
\(\hept{\begin{cases}2k-1=5\\2-1=1\end{cases}\Leftrightarrow k=3}\)
b) Ta có : \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\kx-1-x=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\x\left(k-1\right)=6\end{cases}}\)
Để hệ phương trình có nghiệm duy nhất : \(\Leftrightarrow k-1\ne0\) \(\Leftrightarrow k\ne1\)
Để hệ phương trình vô nghiệm \(\Leftrightarrow k-1=0\Leftrightarrow k=1\)
P/s : Em chưa học lớp 9 nên không biết cách trình bày cho lắm :))