Xét các số thực dương a, b thỏa mãn l o g 2 1 - a b a + b = 2 a b + a + b - 3 . Tìm giá trị nhỏ nhất P m i n của P= a+2b
A. P m i n = 2 10 - 3 2
B. P m i n = 3 10 - 7 2
C. P m i n = 2 10 - 1 2
D. P m i n = 2 10 - 5 2
xét các số thực dương a,b thỏa mãn a+b=2. Tìm max của biểu thức P=a^2*b
Lời giải:
Áp dụng BĐT Cô-si:
\(2=a+b=\frac{a}{2}+\frac{a}{2}+b\geq 3\sqrt[3]{\frac{a^2b}{4}}\)
\(\Rightarrow \frac{2}{3}\geq \sqrt[3]{\frac{a^2b}{4}}\Rightarrow \frac{8}{27}\geq \frac{a^2b}{4}\)
\(\Leftrightarrow a^2b\leq \frac{32}{27}\Leftrightarrow P\leq \frac{32}{27}\)
Vậy $P_{\max}=\frac{32}{27}$. Giá trị này đạt tại $\frac{a}{2}=b=\frac{2}{3}$
xét các số thực dương a,b thỏa mãn a+b=2 . tìm Max của biểu thức P=a2b
Xét các số thực dương \(a,b,c\) thỏa mãn \(abc=a+b+c+2\). CMR:
$$\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\le \dfrac{3}{4}$$
Xét các số thực dương a,b thỏa mãn: log9a = log12b = log15(a+b). Tính \(\dfrac{a}{b}\)
Đặt \(log_9a=log_{12}b=log_{15}\left(a+b\right)=t\Rightarrow\left\{{}\begin{matrix}a=9^t\\b=12^t\\a+b=15^t\end{matrix}\right.\)
\(\Rightarrow9^t+12^t=15^t\)
\(\Rightarrow\left(\dfrac{3}{5}\right)^t+\left(\dfrac{4}{5}\right)^t=1\)
Hàm \(f\left(t\right)=\left(\dfrac{3}{5}\right)^t+\left(\dfrac{4}{5}\right)^t\) có \(f'\left(t\right)=\left(\dfrac{3}{5}\right)^tln\left(\dfrac{3}{5}\right)+\left(\dfrac{4}{5}\right)^t.ln\left(\dfrac{4}{5}\right)< 0\Rightarrow\) nghịch biến trên R
\(\Rightarrow f\left(t\right)\) có tối đa 1 nghiệm \(\Rightarrow t=2\) là nghiệm duy nhất
\(\Rightarrow\dfrac{a}{b}=\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16}\)
xét hai số thực dương a,b thỏa mãn \(a^2\)+\(b^2\)=2 tìm giá trị nhỏ nhất của biểu thức P=\(\dfrac{a^2}{b+1}\)+\(\dfrac{b^2}{a+1}\)
Ta thấy \(ab\le\dfrac{a^2+b^2}{2}=1\) và \(a+b\le\sqrt{2\left(a^2+b^2\right)}=2\). Áp dụng BĐT B.C.S, ta được \(P=\dfrac{a^4}{ba^2+a^2}+\dfrac{b^4}{ab^2+b^2}\) \(\ge\dfrac{\left(a^2+b^2\right)^2}{ba^2+ab^2+a^2+b^2}=\dfrac{2^2}{ab\left(a+b\right)+2}\ge\dfrac{4}{1.2+2}=1\)
ĐTXR \(\Leftrightarrow a=b=1\)
Vậy GTNN của P là 1 khi \(a=b=1\)
Các Ctv hoặc các giáo viên helpp ạ
Cho a,b,c là số thực dương không âm thỏa mãn
Cho a,b,c là số thực dương không âm thỏa mãn \(a+b+c=1\) . Chứng minh rằng :
\(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}>10\)
Xét các số thực dương a, b thỏa mãn log 2 1 − ab a + b = 2 ab + a + b − 3 . Tìm giá trị nhỏ nhất P min của P = a + 2 b
A. P min = 2 10 − 3 2 .
B. P min = 3 10 − 7 2 .
C. P min = 2 10 − 1 2 .
D. P min = 2 10 − 5 2 .
Đáp án A
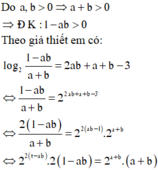
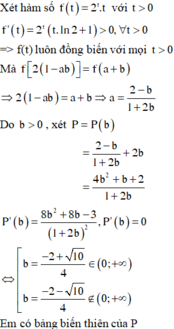
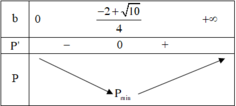
Từ bảng biến thiên em thấy P min = P − 2 + 10 4 = 2 10 − 3 2
1) cho các số thực dương a,b thỏa mãn \(3a+b\le1\). Tìm Min của \(P=\dfrac{1}{a}+\dfrac{1}{\sqrt{ab}}\)
2) Với hai số thực a,b không âm thỏa mãn \(a^2+b^2=4\). Tìm Max \(M=\dfrac{ab}{a+b+2}\)
3) Cho x,y khác 0 thỏa mãn \(\left(x+y\right)xy=x^2+y^2-xy\). Tìm Max \(A=\dfrac{1}{x^3}+\dfrac{1}{y^3}\)
1) Áp dụng bất đẳng thức AM - GM và bất đẳng thức Schwarz:
\(P=\dfrac{1}{a}+\dfrac{1}{\sqrt{ab}}\ge\dfrac{1}{a}+\dfrac{1}{\dfrac{a+b}{2}}\ge\dfrac{4}{a+\dfrac{a+b}{2}}=\dfrac{8}{3a+b}\ge8\).
Đẳng thức xảy ra khi a = b = \(\dfrac{1}{4}\).
2.
\(4=a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\Rightarrow a+b\le2\sqrt{2}\)
Đồng thời \(\left(a+b\right)^2\ge a^2+b^2\Rightarrow a+b\ge2\)
\(M\le\dfrac{\left(a+b\right)^2}{4\left(a+b+2\right)}=\dfrac{x^2}{4\left(x+2\right)}\) (với \(x=a+b\Rightarrow2\le x\le2\sqrt{2}\) )
\(M\le\dfrac{x^2}{4\left(x+2\right)}-\sqrt{2}+1+\sqrt{2}-1\)
\(M\le\dfrac{\left(2\sqrt{2}-x\right)\left(x+4-2\sqrt{2}\right)}{4\left(x+2\right)}+\sqrt{2}-1\le\sqrt{2}-1\)
Dấu "=" xảy ra khi \(x=2\sqrt{2}\) hay \(a=b=\sqrt{2}\)
3. Chia 2 vế giả thiết cho \(x^2y^2\)
\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\ge\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\)
\(\Rightarrow0\le\dfrac{1}{x}+\dfrac{1}{y}\le4\)
\(A=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\right)=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\le16\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
Xét các số thực dương \(a;b\) thay đổi và thỏa mãn : \(a+b\ge2\). Tìm giá trị nhỏ nhất của biểu thức :
\(P=\sqrt{16a^2.b^2+9}.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\).
P/s : Em xin phép đăng bài toán nhờ quý thầy cô giáo và các bạn giúp đỡ, em cám ơn nhiều lắm ạ!
ráng chờ thầy nguyễn việt lâm onl r nhờ nghen:>
\(\sqrt{\left(16+9\right)\left(16a^2b^2+9\right)}\ge\sqrt{\left(16ab+9\right)^2}=16ab+9\)
\(\Rightarrow\sqrt{16a^2b^2+9}\ge\dfrac{1}{5}\left(16ab+9\right)\)
\(\Rightarrow P\ge\dfrac{1}{5}\left(16ab+9\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=\dfrac{1}{5}\left[16\left(a+b\right)+9\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\right]\)
\(P\ge\dfrac{1}{5}\left[32+9.\dfrac{4}{a+b}\right]=\dfrac{1}{5}\left[32+\dfrac{9.4}{2}\right]=10\)
\(P_{min}=10\) khi \(a=b=1\)