Cho hình chóp S.ABC có AB=a,AC= 3 a ,SB>2a và A B C ^ = B A S ^ = B C S ^ = 90 0 . Sin của góc giữa đường thẳng SB và mặt phẳng (SAC) bằng 11 11 . Tính thể tích khối chóp S.ABC.
A. 6 6 a 3
B. 6 3 a 3
C. 3 9 a 3
D. 2 3 9 a 3
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình chóp S.ABC có A B = a , A C = a 3 , S B > 2 a và A B C ^ = B A S ^ = B C S ^ = 90 ∘ . Sin của góc giữa đường thẳng SB và mặt phẳng (SAC) bằng 11 11 . Tính thể tích khối chóp S.ABC

A. 2 3 a 3 9
B. 3 a 3 9
C. 6 a 3 6
D. 6 a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B có AB=BC=a,SB=2a và SA vuông góc với đáy. Tính thể tích khối chóp S.ABC.
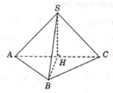
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, đỉnh S cách đều các điểm A,B,C. Biết AC = 2a,BC = a; góc giữa đường thẳng SB và mặt đáy (ABC) bằng 60 o . Tính theo a thể tích V của khối chóp S.ABC?
A. V = a 6 3 4 .
B. V = a 6 3 6 .
C. V = a 3 2 .
D. V = a 6 3 12 .
Đáp án C.
Hướng dẫn giải: Gọi H là trung điểm AC.
Do tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Đỉnh S cách đều các điểm A, B,C nên hình chiếu của S trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC
suy ra S H ⊥ ( A B C )
![]()
Tam giác vuông SBH, có
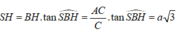
Tam giác vuông ABC ,
có A B = A C 2 - B C 2 = a 3
Diện tích tam giác vuông
S ∆ A B C = 1 2 B A . B C = a 3 2 2
Vậy V S . A B C = 1 3 S ∆ A B C . S H = a 3 2
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, SA = 2a, AB=a; SA vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng AC và SB.
Kẻ BH//AC
AH vuông góc BH tại H
AC//BH
=>d(AC;SB)=d(AC;(SBH))=d(A;(SBH))
Kẻ AK vuông góc SH
=>BH vuông góc (SAH)
=>BH vuông góc AK
=>AK vuông góc (SHB)
=>d(A;(SHB))=AK
ΔABC vuông tại A nên H trùng với B
=>1/AK^2=1/SA^2+1/AB^2
=>AK=2a*căn 5/5
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A,cạnh bên SA vuông góc với đáy (ABC). Biết AB=2a và SB=2 2 a. Tính thể tích V của khối chóp S.ABC?
A. V = 8 a 3 3
B. V = 4 a 3 3
C. V = 4 a 3
D. V = 8 a 3
Đáp án là B
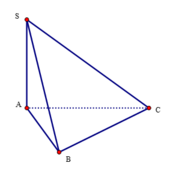
Tam giác SAB vuông tại A có S A 2 = S B 2 - A B 2 = 4 a 2 nên SA= 2a
Có S A B C = 1 2 A B . A C = 2 a 2
Có V = 1 3 S A . S A B C = 4 a 3 3
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Tính thể tích hình chóp S.AB′C′.
A. a 3 2
B. a 3 6
C. a 3 24
D. a 3 12
Cho hình chóp S.ABC có SA ⊥ (ABC), tam giác ABC vuông cân tại B, AC= 2a và SA=a. Gọi M là trung điểm của SB. Tính thể tích khối chóp S.AMC.
A. a 3 9
B. a 3 3
C. a 3 6
D. a 3 12
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Biết SA vuông góc với mặt phẳng đáy và SB = a 10 , BC = 2a, SC = 2a 3 . Thể tích khối chóp S.ABC là:
A . 3 a 3 2
B . 3 a 3 2
C . 3 a 3
D . a 3
Cho hình chóp S.ABC có đáy là tam giác vuông tại B; AB=a, AC=2a, SA vuông góc với mặt phẳng đáy, SA=a. Mặt phẳng (P) đi qua A vuông góc với SC tại H và cắt SB tại K. Thể tích khối chóp S.AHK tính theo a bằng?