Tìm chu kì của hàm số y = 1 cos x
A. T = π
B. T = 2 π
C. T = π 2
D. T = 2 π 3
PB
Những câu hỏi liên quan
1) Tìm giá trị lớn nhất của hàm số y 2 Cos2x + Sin2x 2) Tìm giá trị lớn nhất của hàm số y Sin2018x +Cos2018x3) Tìm chu kì T0 của hàm số f(x) tan2x4) Xác định chu kì của hàm số y Sinx5) Hàm số y Sin2x là hàm số tuần hoàn, có chu kì là bao nhiêuAI GIÚP EM VỚI Ạ, CHỨ EM VÃ LẮM RỒI HUHU. TRÌNH BÀY MỘT XÍU XIU CHO EM HIỂU NỮA THÌ CÀNG TỐT Ạ :(( EM CẢM ƠN NHIỀU LẮM Ạ.
Đọc tiếp
1) Tìm giá trị lớn nhất của hàm số y = 2 Cos2x + Sin2x
2) Tìm giá trị lớn nhất của hàm số y = Sin2018x +
Cos2018x
3) Tìm chu kì T0 của hàm số f(x) = tan2x
4) Xác định chu kì của hàm số y = Sinx
5) Hàm số y = Sin2x là hàm số tuần hoàn, có chu kì là bao nhiêu
AI GIÚP EM VỚI Ạ, CHỨ EM VÃ LẮM RỒI HUHU. TRÌNH BÀY MỘT XÍU XIU CHO EM HIỂU NỮA THÌ CÀNG TỐT Ạ :(( EM CẢM ƠN NHIỀU LẮM Ạ.
Tìm chu kì của hàm số Y=2cot (x/3+π\4)
Hàm số \(y=2cot\left(\dfrac{x}{3}+\dfrac{\pi}{4}\right)\) tuần hoàn với chu kì \(T=\dfrac{\pi}{\left|\dfrac{1}{3}\right|}=3\pi\).
Đúng 0
Bình luận (1)
một chất điểm dao động điều hòa có phương trình là x = 5 cos ( 5 π t + π/ 4 ) ( x tính bằng cm , t tính bằng giây ). dao động này có
A tần số góc 5 rad/s
B chu kì 0.2s
C biên độ 0,05cm
D tần số 2.5Hz
Dao động này có biên độ \(A=5cm\)
Tần số góc là \(5\pi\left(rad/s\right)\)
Chu kì \(T=\dfrac{2\pi}{\omega}=0,4s\)
Và tần số là: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)
⇒ Chọn B
Đúng 2
Bình luận (0)
Một chất điểm dao động điều hoà (dạng hàm cos) có chu kì T, biên độ A. Tốc độ trung bình của chất điểm khi pha của dao động biến thiên từ
-
2
π
/
3
đến
π
/
3
bằng A. 3A/T B. 4A/T C. 3,6A/T D. 2A/T
Đọc tiếp
Một chất điểm dao động điều hoà (dạng hàm cos) có chu kì T, biên độ A. Tốc độ trung bình của chất điểm khi pha của dao động biến thiên từ - 2 π / 3 đến π / 3 bằng
A. 3A/T
B. 4A/T
C. 3,6A/T
D. 2A/T
Cho hàm số
y
cos
2
x
.a) Chứng minh rằng cos
2
x
+
k
π
cos
2
x
với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số
y
cos
2
x
.b) Viết phương...
Đọc tiếp
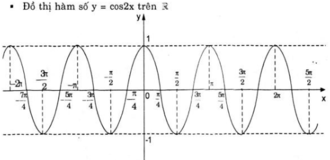
Cho hàm số y = cos 2 x .
a) Chứng minh rằng cos 2 x + k π = cos 2 x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2 x .
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π / 3 .
c) Tìm tập xác định của hàm số : z = 1 - cos 2 x 1 + cos 2 2 x
a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
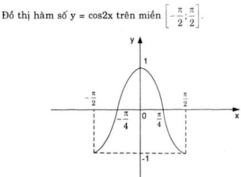
Từ đó suy ra
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
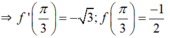
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
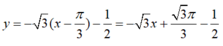
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
⇒ 
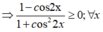
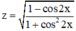luôn xác định với mọi x ∈ R.
Đúng 0
Bình luận (0)
Chứng minh rằng các hàm số sau tuần hoàn và tìm chu kì tuần hoàn của chúng :
a, y= sinx
b, y= sinx + cos x
Tìm chu kì của hàm số y = sin ( 3 x + π / 4 )
A. T= π
B. T=2 π
C. T= π /2
D. T=2 π /3
PH
19 tháng 8 2021 lúc 16:35
hàm số y=Cos(Sinx) có chu kì T là bao nhiêu?
Ta có \(y\left(x+\pi\right)=cos\left[sin\left(x+\pi\right)\right]=cos\left(-sinx\right)=cos\left(sinx\right)\)
nên \(y\left(x+2\pi\right)=y\left(x\right)\)
Tuần hoàn với chu kì π
Đúng 0
Bình luận (0)
TXĐ: \(D=R\)
Với mọi \(x\in R\) thì \(x+\pi\in R\)
Ta có:
\(f\left(x\right)=cos\left(sinx\right)\)
\(f\left(x+\pi\right)=cos\left(sin\left(x+\pi\right)\right)=cos\left(-sinx\right)=cos\left(sinx\right)=f\left(x\right)\)
\(\Rightarrow\) Hàm tuần hoàn với chu kì \(T=\pi\)
Giả sử tồn tại \(0< T_0< \pi\) sao cho \(f\left(x+T_0\right)=f\left(x\right)\); \(\forall x\)
\(\Leftrightarrow cos\left[sin\left(x+T_0\right)\right]=cos\left(sinx\right)\)
Thay \(x=0\Rightarrow cos\left(sinT_0\right)=cos0=1\) (1)
Do \(0< T_0< \pi\Rightarrow0< sinT_0< 1\Rightarrow cos\left(sinT_0\right)< 1\)
\(\Rightarrow\) (1) sai hay điều giả sử là sai
Vậy \(T=\pi\) là chu kì của hàm đã cho
Đúng 0
Bình luận (0)
tìm chu kì của hàm số
f(x)= cos^2 x
f(x)=|cos x|
Mọi người giúp mình giải bài tập này với ạ:
BT: Một Một vật dao động điều hòa có phương trình: x = 2.cos(4πt + π/6 )cm
a) Xác định biên độ chu kì, tần số góc, pha ban đầu của dao động
b) tính li độ X ở thời điểm t = 1/6 (s)
Xem chi tiết
Trời ơi, mình mới học lớp 6 thui