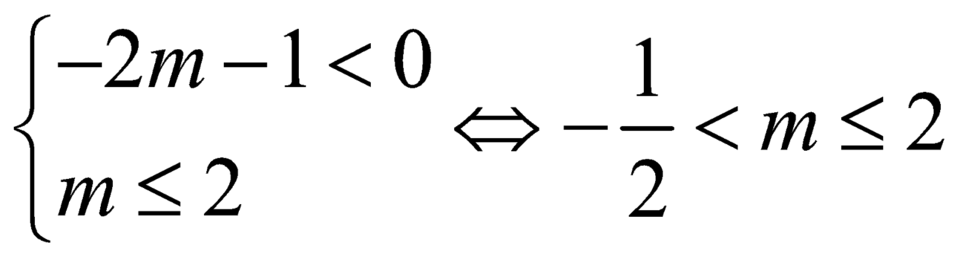Hỏi có bao nhiêu số nguyên m để hàm số y = m 2 − 1 x 3 + m − 1 x 2 − x + 4 nghịch biến trên − ∞ ; + ∞ ?
A. 2
B. 1
C. 0
D. 3
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Hỏi có bao nhiêu số nguyên m để hàm số y = m 2 - 1 x 3 + m - 1 x 2 - x + 4 nghịch biến trên - ∞ ; + ∞ ?
A. 2
B. 1
C. 0
D. 3
Cho hàm số \(y=-2x^3+(2m-1)x^2-(m^2-1)x+2\). Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có hai điểm cực trị?
\(y'=-6x^2+2\left(2m-1\right)x-\left(m^2-1\right)\)
Hàm có 2 cực trị khi:
\(\Delta'=\left(2m-1\right)^2-6\left(m^2-1\right)>0\)
\(\Rightarrow-2m^2-4m+7>0\)
\(\Rightarrow-\dfrac{2+3\sqrt{2}}{2}< m< \dfrac{-2+3\sqrt{2}}{2}\)
\(\Rightarrow m=\left\{-3;-2;-1;0;1\right\}\)
Hỏi có bao nhiêu số nguyên m để hàm số \(y=\left(m^2-1\right)x^3+\left(m-1\right)x^2-x+4\) nghịch biến trên khoảng (-∞;+∞)
Hỏi có bao nhiêu số nguyên m để hàm số y = m 2 - 1 x 3 + m - 1 x 2 - x + 4 nghịch biến trên khoảng (-¥,+¥)?
A. 1
B. 3
C. 2
D. 0
Hỏi có bao nhiêu số nguyên m để hàm số y = 1 3 m - 2 x 3 + m - 2 x 2 - 2 x + 4 nghịch biến trên khoảng ?
A. 0
B. 3
C. 1
D. 2
Đáp án D
Ta có: y ' = m - 2 x 2 + 2 m - 2 x - 2 . Với m = 2 ⇒ y ' = - 2 < 0 nên thỏa mãn.
Với m ≠ 2 ta có để y ' ≤ 0 ⇔ m - 2 > 0 ∆ ' < 0 ⇔ m < 2 ( m - 2 ) 2 + 2 ( m - 2 ) < 0 ⇒ 0 < m < 2
Hợp hai trường hợp suy ra 0 < m ≤ 2 ⇒ m = 1 ; m = 2 .
Cho hàm số y = 1 3 x 3 − 2 x 2 + m − 1 x + 3 . Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số có đúng 5 điểm cực trị?
A. 5
B. 4
C. 6
D. 3
Đáp án D
Nhắc lại quy tắc vẽ đồ thị hàm số y = f x từ đồ thị hàm số y = f x
- Phần 1: Giữ nguyên phần đồ thị hàm số y = f x bên phải trục Oy (bỏ phần bên trái)
- Phần 2: Lấy đối xứng phần đồ thị hàm số y = f x bên phải trục O qua trục O
- Hợp của 2 phần, ta được đồ thị hàm số y = f x
Xét y = f x = 1 3 x 3 − 2 x 2 + m − 1 x + 3 với f x = 1 3 x 3 − 2 x 2 + m − 1 x + 3
Để hàm số y = f x có 5 điểm cực trị ⇔ y = f x có 2 điểm cực trị nằm phía bên phải trục Oy ⇔ f ' x = 0 có 2 nghiệm dương phân biệt ⇔ x 2 − 4 x + m − 1 = 0 có 2 nghiệm dương phân biệt x 1 , x 2
⇔ Δ > 0 x 1 + x 2 > 0 x 1 x 2 > 0 ⇔ 5 − m > 0 m − 1 > 0 ⇔ 1 < m < 5 . Kết hợp m ∈ ℤ → m = 2 ; 3 ; 4
Cho hàm số y = x mũ 4 trừ 2 m bình x bình + 1 Hỏi có tất cả bao nhiêu số nguyên m để đồ thị hàm số có 2 điểm cực tiểu đều thuộc trục hoành. Giúp minh với
3. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\dfrac{x+1}{x+3m}\) nghịch biến trên khoảng(6;+\(\infty\) )?
4. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\dfrac{x+2}{x+3m}\) đồng biến trên khoảng (-\(\infty\);-6)?
3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)
Cho hàm số y = 2 x + 1 x - m với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng 2 ; + ∞
A. 1
B. 2
C. 3
D. 4
Đáp án C
+ 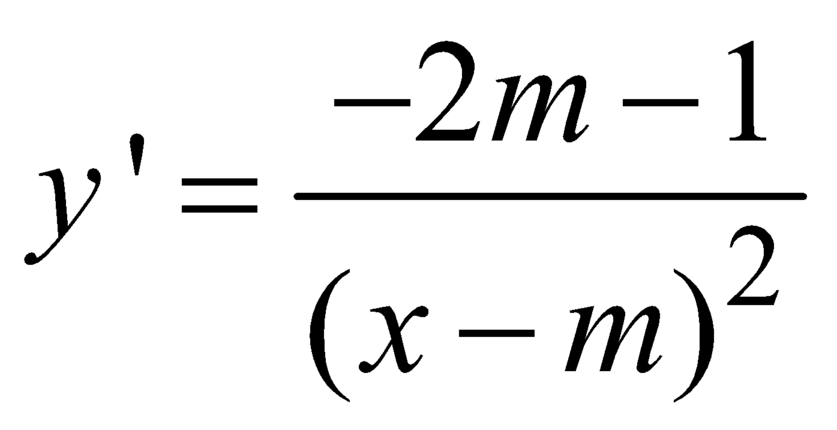
+ Hàm số nghịch biến trên khoảng ![]() khi
khi