Chọn khẳng định sai trong các khẳng định sau:
A. Hàm số y = log 2 x đồng biến trên R
B. Hàm số y = log 1 2 x nghịch biến trên tập xác định của nó
C. Hàm số y = 2 x đồng biến trên R
D. Hàm số y = x 2 có tập xác định là ( 0 ; + ∞ )
Cho hàm số y = f(x) có bảng biến thiên như sau
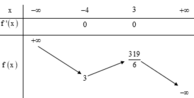
Và các khẳng định sau đây:
(1). Hàm số đồng biến trên (-3;4) (2). Hàm số tăng trên 3 ; 319 6
(3). Hàm số giảm trên − ∞ ; − 4 ∪ 3 ; + ∞ (4). Hàm số giảm trên 3 ; + ∞
Tìm số khẳng định sai trong các khẳng định trên?
A. 1
B. 2
C. 3
D. 4
Câu 1: Cho hàm số y=x-1 Trong các khẳng định sau, khẳng định nào sai?
A. Đồ thị cắt: trục hoành tại A ( 1;0 ) , trục tung tại B (0; -1) .
B.Hàm số đồng biến trên R .
C. Đồ thị không qua gốc tọa độ.
D.Hàm số nghịch biến trên R
D sai, vì hệ số góc $a=1>0$, khi $x$ tăng (giảm) thì $y$ tương ứng tăng (giảm) nên hàm đồng biến trên $R$
Cho hàm số y = x3 + 3x2 – 9x – 7 . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-3;1) .
B. Hàm số đồng biến trên (-9;-5).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên (5;+∞).
Tập xác định: D = R.
Ta có: 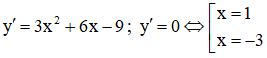
Bảng biến thiên:
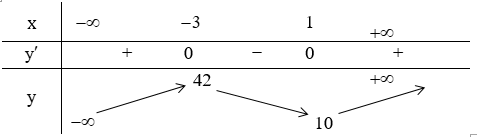
Kết luận: Hàm số đồng biến trên các khoảng: (-∞;-3),(1;+∞) . Hàm số nghịch biến trên khoảng (-3;1)
Chọn C.
Cho các khẳng định:
(I) : Hàm số y=2 đồng biến trên R.
(II) : Hàm số y = x 3 - 12 x nghịch biến trên khoảng (-1;2).
(III): Hàm số y = 2 x - 5 x - 2 đồng biến trên các khoảng - ∞ ; 2 và 2 ; + ∞ .
Trong các khẳng định trên có bao nhiêu khẳng định đúng?
![]()
![]()
![]()
![]()
Cho hàm số y = log 2 x 2 - 2 x - 3 . Xét các khẳng định sau
(I) Hàm số đồng biến trên R
(II) Hàm số đồng biến trên khoảng 3 ; + ∞
(III) Hàm số nghịch biến trên khoảng - ∞ ; - 1
Trong các khẳng định (I), (II) và (III) có bao nhiêu khẳng định đúng
A. 1
B. 2
C. 0
D. 3
Cho hàm số y = f x xác định, liên tục và có đạo hàm trên đoạn a , b . Xét các khẳng định sau:
1. Hàm số f x đồng biến trên a ; b thì f ' x > 0 , ∀ x ∈ a ; b
2. Giả sử f a > f c > f b , ∀ x ∈ a ; b suy ra hàm số nghịch biến trên a ; b
3. Giả sử phương trình f ' x = 0 có nghiệm là x = m khi đó nếu hàm số y = f x đồng biến trên m ; b thì hàm số y = f x nghịch biến trên a , m
4. Nếu f ' x ≥ 0 , ∀ x ∈ a ; b , thì hàm số đồng biến trên a ; b
Số khẳng định đúng trong các khẳng định trên là
A. 1
B. 0
C. 3
D. 2
Đáp án A
Phương pháp:
Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định.
Cách giải:
*2 sai vì với c 1 < c 2 bất kỳ nằm trong a ; b ta chưa thể so sánh được f c 1 và f c 2
*3 sai. Vì y' bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số y = x 3
*4 sai: Vì thiếu điều kiện tại f ' x = 0 hữu hạn điểm.VD hàm số y = 1999 có y ' = 0 ≥ 0 nhưng là hàm hằng.
Chú ý khi giải:
HS thường nhầm lẫn:
- Khẳng định số 4 vì không chú ý đến điều kiện bằng 0 tại hữu hạn điểm.
- Khẳng định số 3 vì không chú ý đến điều kiện đổi dấu qua nghiệm.
trong các khẳng định sau , khẳng định nào đúng ?khẳng định nào sai ? giải thích vì sao ?
a) trên mỗi khoảng mà hàm số y = \(\sin\)x đồng biến thì hàm số y = \(\cos\)x nghịch biến .
b) trên mỗi khoảng mà hàm số y = \(\sin\)2x đồng biến thì hàm số y = \(\cos\)2x nghịch biến
Cho f(x), g(x) là các hàm liên tục trên R. Chọn khẳng định sai trong các khẳng định sau đây
A. ∫ a b f x g x d x = ∫ a b f x d x . ∫ a b g x d x
B. ∫ a b f x + g x d x = ∫ a b f x d x + ∫ a b g x d x
C. ∫ a b f x d x = ∫ a c f x d x + ∫ c b f x d x a < b < c
D. ∫ a b f x - g x d x = ∫ a b f x d x - ∫ a b g x d x
Chọn A
Ta có ngay A sai câu lý thuyết)
trong các khẳng định sau , khẳng định nào đúng ?khẳng định nào sai ? giải thích vì sao ?
a) trên mỗi khoảng mà hàm số y = \(\sin\)x đồng biến thì hàm số y = \(\cos\)x nghịch biến .
b) trên mỗi khoảng mà hàm số y = \(\sin\)2x đồng biến thì hàm số y = \(\cos\)2x nghịch biến .
trong các khẳng định sau , khẳng định nào đúng ?khẳng định nào sai ? giải thích vì sao ?
a) trên mỗi khoảng mà hàm số y = \(\sin x\) đồng biến thì hàm số y = \(\cos x\) nghịch biến .
b) trên mỗi khoảng mà hàm số y = \(\sin^2x\) đồng biến thì hàm số y = \(\cos^2x\) nghịch biến