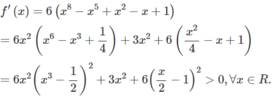Chứng minh rằng f′(x) = 0 ∀x ∈ R , nếu: f ( x ) = cos 6 x + 2 sin 4 x . cos 2 x + 3 sin 2 x . cos 4 x + sin 4 x
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PB
Những câu hỏi liên quan
Bài tập 3: Cho hàm số
f( x )=c o s x. Chứng minh rằng:
2f'(x+pi/3).f'(x-pi/6)=f'(0)-f(2x+pi/6)
Bài tập 4: Cho hàm số y=3(sin^4 x +cos^4 )-2(sin^6 x +cos^6 x). Chứng minh rằng: y'=0 \-/ x€ Z
Bài tập 5: Cho hàm số
Y= (sin x/ 1+cos x)^3. CMR: y'.sinx-3y=0
3.
\(f\left(x+\frac{\pi}{3}\right)=cos\left(x+\frac{\pi}{3}\right)\Rightarrow f'\left(x+\frac{\pi}{3}\right)=-sin\left(x+\frac{\pi}{3}\right)\)
\(f'\left(x-\frac{\pi}{6}\right)=-sin\left(x-\frac{\pi}{6}\right)\)
\(f'\left(0\right)=-sin\left(0\right)=0\)
\(2f'\left(x+\frac{\pi}{3}\right).f'\left(x-\frac{\pi}{6}\right)=2sin\left(x+\frac{\pi}{3}\right)sin\left(x-\frac{\pi}{6}\right)\)
\(=cos\left(\frac{\pi}{2}\right)-cos\left(2x+\frac{\pi}{6}\right)=-cos\left(2x+\frac{\pi}{6}\right)\)
\(f'\left(0\right)-f\left(2x+\frac{\pi}{6}\right)=0-cos\left(2x+\frac{\pi}{6}\right)=-cos\left(2x+\frac{\pi}{6}\right)\)
\(\Rightarrow2f'\left(x+\frac{\pi}{3}\right)f'\left(x-\frac{\pi}{6}\right)=f'\left(0\right)-f\left(2x+\frac{\pi}{6}\right)\) (đpcm)
4.
\(y=3\left(sin^4x+cos^4x\right)-2\left(sin^6x+cos^6x\right)\)
\(=3\left(sin^2x+cos^2x\right)^2-6sin^2x.cos^2x-2\left(sin^2x+cos^2x\right)^3+6sin^2x.cos^2x\left(sin^2x+cos^2x\right)\)
\(=3-2=1\)
\(\Rightarrow y'=0\) ; \(\forall x\)
5.
\(y=\left(\frac{sinx}{1+cosx}\right)^3=\left(\frac{sinx\left(1-cosx\right)}{1-cos^2x}\right)^3=\left(\frac{sinx\left(1-cosx\right)}{sin^2x}\right)^3=\left(\frac{1-cosx}{sinx}\right)^3\)
\(y'=3\left(\frac{1-cosx}{sinx}\right)^2\left(\frac{sin^2x-cosx\left(1-cosx\right)}{sin^2x}\right)=3\left(\frac{1-cosx}{sinx}\right)^2\left(\frac{1-cosx}{sin^2x}\right)=\frac{3\left(1-cosx\right)^3}{sin^4x}\)
\(\Rightarrow y'.sinx-3y=\frac{3\left(1-cosx\right)^3}{sin^3x}-3\left(\frac{1-cosx}{sinx}\right)^3=0\) (đpcm)
Đúng 2
Bình luận (0)
Chứng minh rằng f′(x) > 0 ∀x ∈ R, nếu f ( x ) = 2 x + sin x
Chứng minh rằng f′(x) 0 ∀x ∈ R, nếu
f
(
x
)
2
3
x
9
-
x
6
+
2
x
3
-
3
x
2
+
6
x
-
1
Đọc tiếp
Chứng minh rằng f′(x) > 0 ∀x ∈ R, nếu f ( x ) = 2 3 x 9 - x 6 + 2 x 3 - 3 x 2 + 6 x - 1
Chứng minh rằng f′(x) 0 ∀x ∈ R , nếu:
f
(
x
)
3
(
sin
4
x
+
cos
4
x
)
−
2
(
sin
6
x
+
cos
6
x
)
Đọc tiếp
Chứng minh rằng f′(x) = 0 ∀x ∈ R , nếu: f ( x ) = 3 ( sin 4 x + cos 4 x ) − 2 ( sin 6 x + cos 6 x )
Chứng minh các biểu thức đã cho không phụ thuộc vào x.
f(x) = 1 ⇒ f′(x) = 0
Đúng 0
Bình luận (0)
Chứng minh rằng fleft(xright)0;forall xin R nếu :
a) fleft(xright)3left(sin^4x+cos^4xright)-2left(sin^6x+cos^6xright)
b) fleft(xright)cos^6x+2sin^4x.cos^2x+3sin^2xcos^4x+sin^4x
c) fleft(xright)cosleft(x-dfrac{pi}{3}right)cosleft(x+dfrac{pi}{4}right)+cosleft(x+dfrac{pi}{6}right)cosleft(x+dfrac{3pi}{4}right)
d) fleft(xright)cos^2x+cos^2left(dfrac{2pi}{3}+xright)+cos^2left(dfrac{2pi}{3}-xright)
Đọc tiếp
Chứng minh rằng \(f'\left(x\right)=0;\forall x\in R\) nếu :
a) \(f\left(x\right)=3\left(\sin^4x+\cos^4x\right)-2\left(\sin^6x+\cos^6x\right)\)
b) \(f\left(x\right)=\cos^6x+2\sin^4x.\cos^2x+3\sin^2x\cos^4x+\sin^4x\)
c) \(f\left(x\right)=\cos\left(x-\dfrac{\pi}{3}\right)\cos\left(x+\dfrac{\pi}{4}\right)+\cos\left(x+\dfrac{\pi}{6}\right)\cos\left(x+\dfrac{3\pi}{4}\right)\)
d) \(f\left(x\right)=\cos^2x+\cos^2\left(\dfrac{2\pi}{3}+x\right)+\cos^2\left(\dfrac{2\pi}{3}-x\right)\)
Chứng minh các biểu thức đã cho không phụ thuộc vào x.
Từ đó suy ra f'(x)=0
a) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
b) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
c) f(x)=\(\frac{1}{4}\)(\(\sqrt{2}\)-\(\sqrt{6}\))=>f'(x)=0
d,f(x)=\(\frac{3}{2}\)=>f'(x)=0
Chứng minh rằng hàm số f(x) = cos(1/x) không có giới hạn khi x → 0
Chọn hai dãy số có số hạng tổng quát là 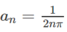 và
và 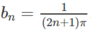 .
.
Tính và so sánh lim f ( a n ) và lim f ( b n ) để kết luận về giới hạn của f(x) khi x → 0
Đúng 0
Bình luận (0)
Bài 5: Cho hàm số y=f(x)≠0y=f(x)≠0 (∀x∈R;x≠0∀x∈R;x≠0) có tính chất f(x1,x2)=f(x1).f(x2)f(x1,x2)=f(x1).f(x2) . Hãy chứng minh rằng:
a) f(1)=1f(1)=1 b) f(x−1)=[f(x)]−1
giúp mình phần b với!
a,Cho đa thức f(x)=ax+b (a khác 0). Biết f(0)=0, chứng minh rằng F(x)=-f(-x)với mọi x
b,Đa thức f(x)=ax^2=bx+c (a khác 0).Biết F(1)=F(-1), chứng minh rằng f(x) với mọi x
Cho đa thức f(x) = ax^2 + bx + c ( a, b, c là hằng số ). Chứng minh rằng
a) Nếu a + b + c = 0 thì f(x) có một nghiệm x=1
b) Nếu a - b + c = 0 thì f(x) có một nghiệm x= -1
c) Nếu f(1) = f(-1) thì f(x) = f(-x) với mọi x
Bài làm
a) Giả sử P(x) có một nghiệm là 1 thì:
p(1)=a*1^2+b*1+c
=a+b+c
Mà a+b+c=0
=>p(1)=0
=>đa thức p(x) có 1 nghiệm là 1(ĐPCM)
b)Giả sử P(x) có 1 nghiệm là -1 thì
p(-1)=a*(-1)^2+b*(-1)+c
=a-b+c
Mà a-b+c=0
=>p(-1)=0
=> đa thức p(x) có một nghiệm là -1(ĐPCM)
c)TA có:
p(1)=a*1^2+b*1+c=a+b+c
p(-1)=a.(-1)^2+b*(-1)+c=a-b+c
Mà p(1)=p(-1)
=>a+b+c=a-b+c
=>a+b+c-a+b-c=0
=>2b=0 =>b=0
+) Với b=0 =>p(x)=ax^2+c (1)
=>p(-x)=a*(-x)^2+c=a*x+c (2)
Từ (1)và (2) =>p(x)=p(-x) (ĐPCM)
Đúng 0
Bình luận (0)