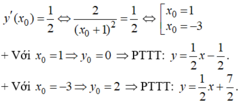Ta có: Với mọi x0 ≠ 0:

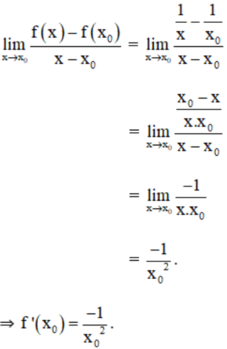
b) Tại x0 = -1

⇒ y0 = -1

⇒ f’(x0) = -1.

Vậy phương trình tiếp tuyến của đường cong 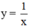 tại điểm có hoành độ -1 là:

y = -1(x + 1) – 1 = -x – 2.

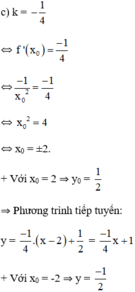
⇒ Phương trình tiếp tuyến:

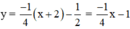
Vậy có hai phương trình tiếp tuyến của hypebol 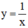 có hệ số góc  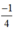bằng

a) Ta có \(2a = 20 \Rightarrow a = 10,2b = 16 \Rightarrow b = 8\).

Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)

b) Ta có \(2a = 12 \Rightarrow a = 6,2c = 20 \Rightarrow c = 10\), suy ra \(b = \sqrt {{c^2} - {a^2}}  = \sqrt {{{10}^2} - {6^2}}  = 8\)

Vậy phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{64}} = 1\)

c) Ta có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\).

Do đó, \(\frac{p}{2} = \frac{1}{2}\) suy ra \(p = 1\).

Vậy phương trình chính tắc của parabol là \({y^2} = 2x\).

Ta có: \(4{x^2}-9{y^2} = {\rm{ }}1 \Leftrightarrow \frac{{{x^2}}}{{{{\left( {\frac{1}{4}} \right)}^2}}} - \frac{{{y^2}}}{{{{\left( {\frac{1}{9}} \right)}^2}}} = 1\)

Vậy phương trình chính tắc của hypebol là: \(\frac{{{x^2}}}{{{{\left( {\frac{1}{4}} \right)}^2}}} - \frac{{{y^2}}}{{{{\left( {\frac{1}{9}} \right)}^2}}} = 1\)

a, Phương trình tiếp tuyến đi qua M: \(ax+by-3a+b=0\left(\Delta\right)\)

Đường tròn đã cho có tâm \(I=\left(1;-2\right)\) bán kính \(R=\sqrt{5}\)

Ta có: \(d\left(I;\Delta\right)=\dfrac{\left|a-2b-3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{5}\)

\(\Leftrightarrow\left(2a+b\right)^2=5\left(a^2+b^2\right)\)

\(\Leftrightarrow\left(a-2b\right)^2=0\)

\(\Leftrightarrow a=2b\)

\(\Rightarrow\Delta:2x+y-5=0\)

b, Phương trình tiếp tuyến: \(\left(d\right)2x-y+m=0\left(m\in R\right)\)

Ta có: \(d\left(I;d\right)=\dfrac{\left|2.1-1.\left(-2\right)+m\right|}{\sqrt{5}}=\sqrt{5}\)

\(\Leftrightarrow\left|m+4\right|=5\)

\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-9\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}d:2x-y+1=0\\d:2x-y-9=0\end{matrix}\right.\)

1.

Tạo với Ox là tạo với tia Ox hay trục hoành nhỉ? 2 cái này khác nhau đấy. Tạo với tia Ox thì chỉ có 1 góc 60 độ theo chiều dương, tạo với trục hoành thì có 2 góc 60 và 120 đều thỏa mãn. Coi như tạo tia Ox đi

Đường tròn tâm \(I\left(-2;-2\right)\) bán kính \(R=5\)

\(tan60^0=\sqrt{3}\Rightarrow\) tiếp tuyến có hệ số góc bằng \(\sqrt{3}\Rightarrow\) pt có dạng:

\(y=\sqrt{3}x+b\Leftrightarrow\sqrt{3}x-y+b=0\)

\(d\left(I;d\right)=R\Leftrightarrow\dfrac{\left|-2\sqrt{3}+2+b\right|}{\sqrt{3+1}}=5\)

\(\Leftrightarrow\left|b+2-2\sqrt{3}\right|=10\Rightarrow\left[{}\begin{matrix}b=8+2\sqrt{3}\\b=-12+2\sqrt{3}\end{matrix}\right.\)

Có 2 tiếp tuyến: \(\left[{}\begin{matrix}\sqrt{3}x-y+8+2\sqrt{3}=0\\\sqrt{3}x-y-12+2\sqrt{3}=0\end{matrix}\right.\)

2.

(C1) có tâm \(I\left(1;1\right)\) bán kính \(R_1=\sqrt{2}\)

(C2) có tâm \(J\left(2;3\right)\) bán kính \(R_2=4\)

Gọi tiếp tuyến chung d có pt: \(ax+by+c=0\)

\(\left\{{}\begin{matrix}d\left(I;d\right)=R_1\\d\left(J;d\right)=R_2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{\left|a+b+c\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\\\dfrac{\left|2a+3b+c\right|}{\sqrt{a^2+b^2}}=4\end{matrix}\right.\)

\(\Rightarrow2\sqrt{2}\left|a+b+c\right|=\left|2a+3b+c\right|\)

? Đề nghiêm túc đấy chứ? Cho kiểu này thì sấp mặt, tối thiểu pt (C1) cũng có dạng \(x^2+y^2-2x-2y+1=0\) để học sinh còn thở chứ.

Ủa, nhìn lại thì bài 2 người ta cho đề kiểu hack não.

\(\overrightarrow{IJ}=\left(1;2\right)\Rightarrow IJ=\sqrt{5}< R_2-R_1=4-\sqrt{2}\)

Do đó \(\left(C_2\right)\) chứa \(\left(C_1\right)\) nên ko tồn tại tiếp tuyến chung của 2 đường tròn

\(y'=\dfrac{-1}{\left(x-1\right)^2}\)

Gọi tiếp tuyến qua điểm \(M\left(a;b\right)\) thuộc (C) có dạng:

\(y=\dfrac{-1}{\left(a-1\right)^2}\left(x-a\right)+\dfrac{2a-1}{a-1}\)

\(\Leftrightarrow x+\left(a-1\right)^2y-2a^2+2a-1=0\)

Áp dụng công thức khoảng cách:

\(\dfrac{\left|1+2\left(a-1\right)^2-2a^2+2a-1\right|}{\sqrt{1+\left(a-1\right)^4}}=\sqrt{2}\)

\(\Leftrightarrow\left|2a-2\right|=\sqrt{2}.\sqrt{1+\left(a-1\right)^4}\)

\(\Leftrightarrow2\left(a-1\right)^2=1+\left(a-1\right)^4\)

\(\Leftrightarrow\left[\left(a-1\right)^2-1\right]^2=0\Rightarrow a=...\)

b.

Vẫn từ công thức khoảng cách trên:

\(d=\dfrac{\left|2a-2\right|}{\sqrt{1+\left(a-1\right)^4}}=\dfrac{2\sqrt{\left(a-1\right)^2}}{\sqrt{1+\left(a-1\right)^4}}=\dfrac{2}{\sqrt{\dfrac{1}{\left(a-1\right)^2}+\left(a-1\right)^2}}\)

\(d\le\dfrac{2}{\sqrt{2\sqrt{\dfrac{\left(a-1\right)^2}{\left(a-1\right)^2}}}}=\sqrt{2}\)

Vậy \(d_{max}=\sqrt{2}\) khi tiếp tuyến trùng với các tiếp tuyến câu a

a) Ta có:

Suy ra phương trình tiếp tuyến cần tìm là:

y – 3 = -2(x – 2) ⇔ y = -2x + 7

b) Ta có: y’ = f’(x) = 3x² + 8x ⇒ f’(-1) = 3 – 8 = -5

Mặt khác: x₀ = -1 ⇒ y₀ = -1 + 4 – 1 = 2

Vậy phương trình tiếp tuyến cần tìm là:

y – 2 = -5 (x + 1) ⇔ y = -5x – 3

c) Ta có:

y₀ = 1 ⇒ 1 = x² – 4x + 4 ⇒ x₀² – 4x₀ + 3 = 0 ⇒ x₀ = 1 hoặc x₀ = 3

f’(x) = 2x – 4 ⇒ f’(1) = -2 và f’(3) = 2

Vậy có hai tiếp tuyến cần tìm có phương trình là:

y – 1 = -2 (x – 1) ⇔ y = -2x + 3

y – 1 = 2 (x – 3) ⇔ y = 2x – 5

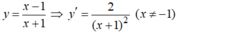
d: 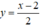 có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.

- Gọi ( x 0 ,   y 0 )  là toạ độ của tiếp điểm.

- Ta có: