(m - 2)x2 + 2(2m - 3)x + 5m - 6 = 0 (1)

- Nếu m - 2 = 0 ⇔ m = 2, khi đó phương trình (1) trở thành:

2x + 4 = 0 ⇔ x = -2 hay phương trình (1) có một nghiệm

Do đó m = 2 không phải là giá trị cần tìm.

- Nếu m - 2 ≠ 0 ⇔ m ≠ 2 ta có:

Δ' = (2m - 3)2 - (m - 2)(5m - 6)

= 4m2 - 12m + 9 - 5m2 + 6m + 10m - 12

= -m2 + 4m - 3 = (-m + 3)(m - 1)

(1) vô nghiệm ⇔ Δ' < 0 ⇔ (-m + 3)(m - 1) < 0 ⇔ m ∈ (-∞; 1) ∪ (3; +∞)

Vậy với m ∈ (-∞; 1) ∪ (3; +∞) thì phương trình vô nghiệm.

a.

Pt có 2 nghiệm pb khi:

\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(-m+2\right)>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\2m^2+7m+7>0\left(\text{luôn đúng}\right)\end{matrix}\right.\) 

\(\Rightarrow m\ne-1\)

b.

BPT vô nghiệm khi \(\left(m^2-4m-5\right)x^2+2\left(m-5\right)-1< 0\) nghiệm đúng với mọi x

- Với \(m=-1\) ko thỏa mãn

- Với \(m=5\) thỏa mãn

- Với \(m\ne\left\{-1;5\right\}\)

\(\Rightarrow\left\{{}\begin{matrix}m^2-4m-5< 0\\\Delta'=\left(m-5\right)^2+m^2-4m-5< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\\left(m-5\right)\left(2m-4\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\2< m< 5\end{matrix}\right.\) \(\Rightarrow2< m< 5\)

Kết hợp lại ta được: \(2< m\le5\)

f(x) = (m + 1) x 2  - 2(3 - 2m)x + m + 1 ≥ 0 (1)

Với m = -1:

(1) ⇔ -10x ≥ 0 ⇔ x ≤ 0

Vậy với m = -1 bất phương trình (1) có nghiệm x ≤ 0

Suy ra, m = -1 (loại)

Với m ≠ -1:

f(x) = (m +1 ) x 2  - 2(3 - 2m)x + m + 1

Δ' = [-(3 - 2m) ] 2  - (m + 1)(m + 1) = (2m - 3 ) 2  - (m + 1 ) 2

= (2m - 3 + m + 1)(2m - 3 - m - 1) = (3m - 2)(m - 4)

Để bất phương trình (1) vô nghiệm thì:

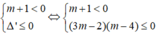
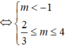
Vậy không có giá trị nào của m để bất phương trình (1) vô nghiệm

  ( m 2 + m + 3 ) x 2 + ( 4 m 2 + m + 2 ) x + m = 0  có a =   m 2   +   m   +   3 > 0, ∀m và có b =   4 m 2   +   m   +   2 > 0, ∀m, nên ab > 0, ∀m. Vì vậy không có giá trị nào của m để phương trình đã cho có hai nghiệm dương phân biệt.

BPT đã cho vô nghiệm khi:

\(-x^2+x-m\le0\) nghiệm đúng với mọi x

\(\Leftrightarrow\Delta'=1-4m\le0\)

\(\Rightarrow m\ge\dfrac{1}{4}\)

TH1: m=-1

BPT sẽ là:

-2(-1-1)x-3-3>0

=>4x-6>0

=>x>6/4

=>Loại
TH2: m<>-1

Δ=(2m-2)^2-4(m+1)(3m-3)

=4m^2-8m+4-4(3m^2-3)

=4m^2-8m+4-12m^2+12

=-8m^2-8m+16

Để BPT vô nghiệm thì -8m^2-8m+16<=0 và m+1<0

=>m^2+m-2>=0 và m<-1

=>(m+2)(m-1)>=0 và m<-1

=>(m>=1 hoặc m<=-2) và m<-1

=>m<=-2

1) điều kiện của m: m khác 5/2

thế x=2 vào pt1 ta đc:

(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)

lập △'=[-(m-1)]²-*(2m-5)*3 = (m-4)²

vì (m-4)² ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2

3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m

\(x^2-2\left(m-1\right)x+4m+8< 0\)

\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(4m+8\right)\)

\(=4m^2-4m+1-16m+32\)

\(=4m^2-20m+33\)

Để BPT vô nghiệm thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4m^2-20m+33< =0\\1>0\left(đúng\right)\end{matrix}\right.\)

=>\(4m^2-20m+33< =0\)

=>\(\left(2m-5\right)^2+8< =0\)(vô lý)

=>\(m\in\varnothing\)

+ Nếu m = 0 thì bất phương trình nghiệm đúng với mọi x;

    + Nếu m = -2 thì bất phương tình trở thành – 4x + 2 > 0, không nghiệm đúng với mọi x.

    + Nếu m ≠ 0 và m ≠ -2 thì bất phương trình nghiệm đúng với mọi x khi và chỉ khi

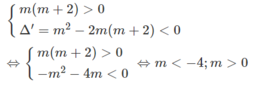
Đáp số: m < -4; m ≥ 0