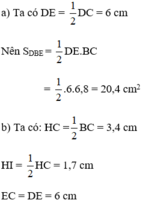Cho tứ diện ABCD. Gọi h A , h B , h C , h D lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh rằng: 1 h A + 1 h B + 1 h C + 1 h D = 1 r
PB
Những câu hỏi liên quan
Trong không gian Oxyz, cho tứ diện đều ABCD có A(0;1;2). Gọi H là hình chiếu vuông góc của A lên mặt phẳng (BCD). Cho H(4;-3;-2). Tọa độ tâm I và bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD là: A. I(2; -1; 0); R 2
3
B. I(4; -3; -2); R 4
3
C. I(3; -2; -1); R 3
3
D. I(3; -2; -1); R 9
Đọc tiếp
Trong không gian Oxyz, cho tứ diện đều ABCD có A(0;1;2). Gọi H là hình chiếu vuông góc của A lên mặt phẳng (BCD). Cho H(4;-3;-2). Tọa độ tâm I và bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD là:
A. I(2; -1; 0); R = 2 3
B. I(4; -3; -2); R = 4 3
C. I(3; -2; -1); R = 3 3
D. I(3; -2; -1); R = 9
Đáp án C
Do ABCD là tứ diện đều nên H là trọng tâm tam giác BCD và I trùng với trọng tâm G của tứ diện ABCD. Ta có:
![]()
![]()
Từ đó ta có:
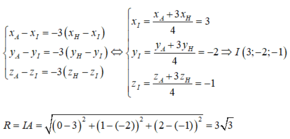
Vậy đáp án C đúng.
Đúng 0
Bình luận (0)
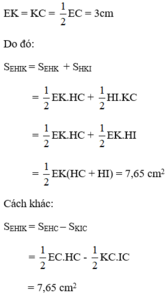
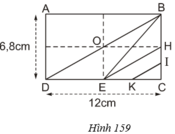
Cho hình chữ nhật ABCD. Gọi H, I, E, K lần lượt là các trung điểm của BC, HC, DC, EC (h.159). Tính
a) Diện tích tam giác DBE
b) Diện tích tứ giác EHIK
Cho tứ diện ABCD. Gọi I và K là trung điểm AB và CD. Gọi J là một điểm trên AD sao cho AD3JD a) Tìm giao điểm F của IJ và (BCD) b) Tìm giao điểm E của BC và (IJK) c) Chứng minh AC, KJ, IE đồng quy tại H Cho tứ diện ABCD. Gọi I và K là trung điểm AB và CD. Gọi J là một điểm trên AD sao cho AD3JD a) Tìm giao điểm F của IJ và (BCD) b) Tìm giao điểm E của BC và (IJK) c) Chứng minh AC, KJ, IE đồng quy tại H d, Chứng minh EJ//HF
Đọc tiếp
Cho tứ diện ABCD. Gọi I và K là trung điểm AB và CD. Gọi J là một điểm trên AD sao cho AD=3JD a) Tìm giao điểm F của IJ và (BCD) b) Tìm giao điểm E của BC và (IJK) c) Chứng minh AC, KJ, IE đồng quy tại H Cho tứ diện ABCD. Gọi I và K là trung điểm AB và CD. Gọi J là một điểm trên AD sao cho AD=3JD a) Tìm giao điểm F của IJ và (BCD) b) Tìm giao điểm E của BC và (IJK) c) Chứng minh AC, KJ, IE đồng quy tại H d, Chứng minh EJ//HF
Cho tứ diện ABCD có ABAC
2
, DBDC
3
, góc giữa hai mặt phẳng (ABC) và (DBC) bằng 45 độ. Gọi H là hình chiếu vuông góc của A trên mặt phẳng (DBC) sao cho H và D nằm về hai phía của BC. Tính diện tích S của mặt cầu ngoại tiếp tứ diện ABCD A.
5
π
B.
5
π
4
C.
S
5
π...
Đọc tiếp
Cho tứ diện ABCD có AB=AC= 2 , DB=DC= 3 , góc giữa hai mặt phẳng (ABC) và (DBC) bằng 45 độ. Gọi H là hình chiếu vuông góc của A trên mặt phẳng (DBC) sao cho H và D nằm về hai phía của BC. Tính diện tích S của mặt cầu ngoại tiếp tứ diện ABCD
A. 5 π
B. 5 π 4
C. S = 5 π 8
D. S = 5 π 16
Cho hình thoi ABCD có AC = 10 cm, BD = 6cm. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA.
a) Tứ giác EFGH là hình gì? Vì sao?
b) Tính diện tích hình thoi ABCD.
c) Tính diện tích tứ giác EFGH.
a) Ta có EFGH là hình chữ nhật (Tứ giác có 3 góc vuông)
b) S A B C D = 1 2 A C . B D = 30 c m 2
c) SEFGH = EF.FG = 15cm2
Đúng 0
Bình luận (0)
Bài 22. Cho hình thang cân ABCD với AB // CD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.
a) Tứ giác MNPQ là hình gì?
b) Cho biết diện tích tứ giác ABCD bằng 60cm2. Tính diện tích tứ giác MNPQ.
Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số : \(\dfrac{V_{\left(H\right)}}{V_{ABCD}}\) ?

Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là \(\dfrac{a}{2}\). Khi đó :
\(V_{ABCD}=a^3\dfrac{\sqrt{2}}{12};V_{\left(H\right)}=\dfrac{1}{3}\left(\dfrac{a}{2}\right)^3\sqrt{2}=a^3\dfrac{\sqrt{2}}{24}\)
Từ đó suy ra :
\(\dfrac{V_{\left(H\right)}}{V_{ }ABCD}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
A
B
A
C
2
,
B
C
2
,
D
B
D
C
3
, góc giữa hai mặt phẳng
A
B
C
và
D
B
C
bằng
45
°...
Đọc tiếp
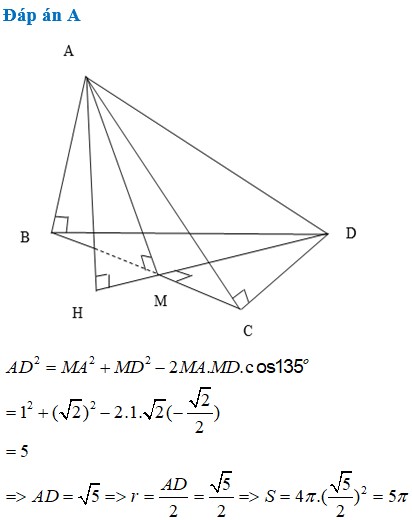
Cho tứ diện ABCD có A B = A C = 2 , B C = 2 , D B = D C = 3 , góc giữa hai mặt phẳng A B C và D B C bằng 45 ° . Gọi H là hình chiếu vuông góc của A trên mặt phẳng D B C sao cho H và D nằm về hai phía của BC. Tính diện tích S của mặt cầu ngoại tiếp tứ giác ABCD.
A. S = 5 π
B. S = 5 π 4
C. S = 5 π 8
D. S = 5 π 16
Chọn A

Phương pháp:
Cách giải:


Mà AH vuông góc (BCD) nên AH là trục của mặt phẳng (BCD).
Gọi K là trung điểm AD, kẻ OK vuông góc với AD, O thuộc AH

Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có BC=2AB. Gọi M,N lần lượt là trung điểm của BC và AD. Gọi P là giao điểm của AM với BN, Q là giao điểm MD với CN.
a)Chứng minh: Tứ giác ABMN là hình thoi.
b)Tứ giác PMQN là hình gì? Tại sao?
c)Chứng minh: Diện tích ABCD=8 lần diện tích PMN
cho tứ giác ABCD gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CD,DA
a/ tứ giác MNPQ là hình gì?
b/ tính điều kiện của tứ giác ABCD để tứ giác MNPQ là hình vuông
c/với điều kiện câu b hãy tính tỉ số diện tích của tứ giác ABCD và tứ giác MNPQ
ta nối AC
xét tam giác ABC có
AM=MB BN=NC
Suy ra MN là đường trung bình
suy ra MN//AC MN=1/2AC (1)
xét tam giác ADC có
AQ=QD DP=PC
Suy ra QP là đường trung bình
suy ra QP//AC QP=1/2AC (2)
Từ 1 và 2 suy ra MN//PQ PQ=MN
suy ra tứ giác MNQP là hình bình hành
Đúng 0
Bình luận (0)