giúp mình với ạ

giúp mình với ạ

Cíuu với ạ :( 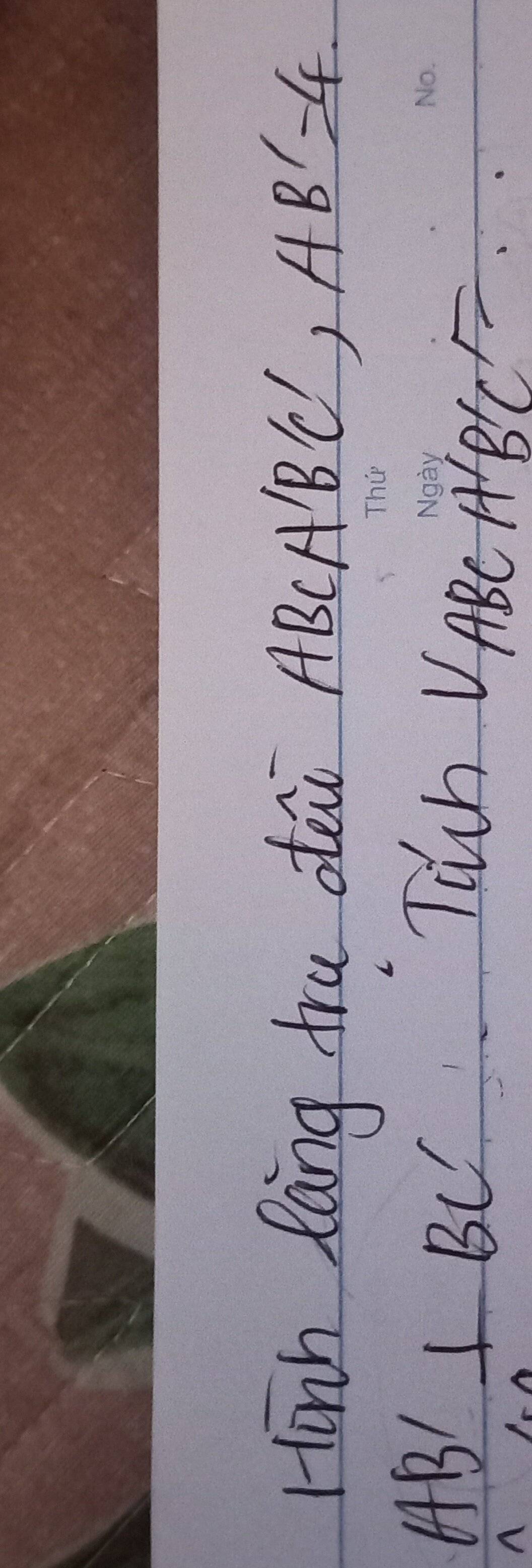
Cho lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác đều cạnh a. số đo của góc giữa 2 mp A'BC vf ABC là 60°. tính thể tích khối lăng trụ ABC. A'B'C'. Giúp mình với ạ
Cho hình chóp tứ giác đều S.ABCD có cạnh bằng a, góc giữa mặt phẳng (SAB) và mặt phẳng (ABCD) bằng 60.Gọi G là trọng tâm tam giác SAC, M thuộc cạnh SB sao cho SM=1/4SB. tính góc giữa 2 đường thẳng GM và BC
Mọi người giúp em giải bài này với em cảm ơn nhìu ạ<3
Cho hình chóp SABCD có đáy là hình bình hành AB=a AD=2a , góc BAD = 60 độ , SA vuông đáy , tính V ,Tỉ số V/a^3
Đề bài thiếu dữ liệu để tính độ dài SA nên không tính được V
Mọi người giúp mình bài 3 với ạ 
Cho mình hỏi bài này ạ câu 11 ạ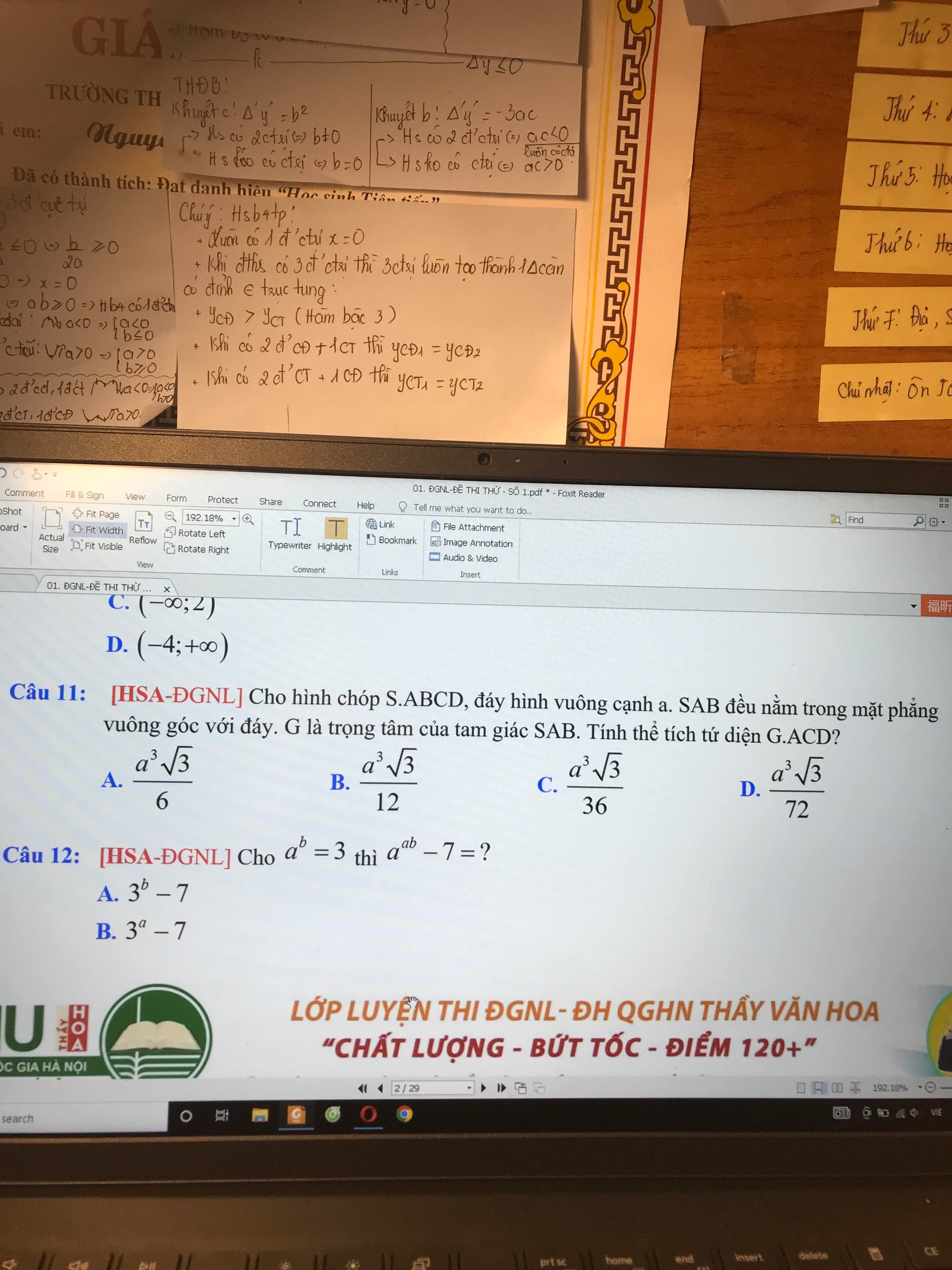
\(d\left(G;\left(ABCD\right)\right)=\dfrac{1}{3}d\left(S;\left(ABCD\right)\right)=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6}\)
\(S_{\Delta ACD}=\dfrac{1}{2}S_{ABCD}=\dfrac{a^2}{2}\)
\(\Rightarrow V=\dfrac{1}{3}.\dfrac{a^2}{2}.\dfrac{a\sqrt{3}}{6}=\dfrac{a^3\sqrt{3}}{36}\)
Cho hình chóp sabcd có đáy là hình vuông cạnh a căn 2 sa vuông với đáy và sb =2a góc giữa sb và mặt phẳng sac bằng
Gọi O là giao điểm AC và BD
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(\Rightarrow BO\perp\left(SAC\right)\) \(\Rightarrow SO\) là hình chiếu vuông góc của SB lên (SAC)
\(\Rightarrow\widehat{BSO}\) là góc giữa SB và (SAC)
\(OB=\dfrac{1}{2}BD=\dfrac{1}{2}.a\sqrt{2}.\sqrt{2}=a\)
\(\Rightarrow sin\widehat{BSO}=\dfrac{OB}{SB}=\dfrac{a}{2a}=\dfrac{1}{2}\)
\(\Rightarrow\widehat{BSO}=30^0\)
Giúp mk với ạ
Đề bài bị sai
Gọi H là trung điểm AB thì \(SH\perp\left(ABCD\right)\Rightarrow\widehat{SCH}=60^0\)
\(\Rightarrow CH=\dfrac{SH}{tan60^0}=\dfrac{SH}{\sqrt{3}}\)
Mặt khác tam giác SAB đều \(\Rightarrow\widehat{SBH}=60^0\Rightarrow BH=\dfrac{SH}{tan60^0}=\dfrac{SH}{\sqrt{3}}\)
\(\Rightarrow CH=BH\) (vô lý do tam giác BCH vuông tại B theo giả thiết. Mà CH là cạnh huyền, BH là cạnh góc vuông, 2 cạnh này không thể bằng nhau)