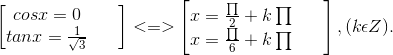Giải phương trình sin x + cos x cos x - sin x = 1 + 2 sin x
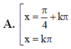
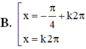
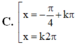
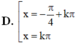
Giải phương trình cos x + cos 3 x = sin x - sin 3 x .
A . x = - π 4 + k π 2 k ∈ ℤ
B . x = π 4 + k π 2 k ∈ ℤ
C . x = π 4 + k π k ∈ ℤ
D . x = π 4 + k 2 π k ∈ ℤ
câu này nhìn ngứa mắt quá làm kiểu gì giờ ???
giải phương trình sin^2 x − 4√3 sin x · cos x + cos^2 x = −2.
Với \(cosx=0\) ko phải nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow tan^2x-4\sqrt{3}tanx+1=-2\left(1+tan^2x\right)\)
\(\Leftrightarrow3tan^2x-4\sqrt{3}tanx+3=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x=\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
Giải phương trình cos 4 x + 12 sin x . cos x - 5 = 0
![]()
![]()
Giải các phương trình: sin x + cos x = 1 + sin x . cos x
sin x + cos x = 1 + sin x.cos x
⇔ sin x.cos x – sin x – cos x + 1 = 0
⇔ (sinx. cosx –sinx)- (cosx -1 ) =0
⇔ sinx. (cosx – 1) – (cosx -1) = 0
⇔ (sin x – 1)(cos x – 1) = 0
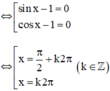
Vậy phương trình có tập nghiệm 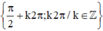
Giải các phương trình sau :
a) \(\cos^2x+2\sin x\cos x+5\sin^2x=2\)
b) \(3\cos^2x-2\sin2x+\sin^2x=1\)
c) \(4\cos^2x-3\sin x\cos x+3\sin^2x=1\)
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Giải phương trình sin(x-50◘)=cos(x+120◘)
\(cos\left(x+120^0\right)=sin\left(x-50^0\right)\)
\(\Leftrightarrow cos\left(x+120^0\right)=cos\left(90^0-\left(x-50^0\right)\right)\)
\(\Leftrightarrow cos\left(x+120^0\right)=cos\left(140^0-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x+120^0=140^0-x+k360^0\\x+120^0=x-140^0+k360^0\left(vn\right)\end{matrix}\right.\)
\(\Leftrightarrow2x=20^0+k360^0\)
\(\Leftrightarrow x=10^0+k180^0\)
Giải phương trình sau:
a) $\tan ^2x+4\cos ^2x+7=4\tan x+8\cot x$
b) $6\sin ^2x+2\cos ^2x-2\sqrt{3}\sin 2x=14\sin \left(x-\frac{\pi }{6}\right)$
Giải phương trình Sin(3x)=Cos(x)
Lời giải:
$\sin 3x= \cos x= \sin (\frac{\pi}{2}-x)$
\(\Leftrightarrow \left[\begin{matrix} 3x=\frac{\pi}{2}-x+2k\pi\\ 3x=\pi -(\frac{\pi}{2}-x)+2k\pi\end{matrix}\right.(k\in\mathbb{Z})\)
\(\Leftrightarrow \left[\begin{matrix} x=\frac{1}{4}(2k+\frac{1}{2})\pi\\ x=\frac{1}{2}(2k+\frac{1}{2})\pi\end{matrix}\right. (k\in\mathbb{Z})\)
Giải các phương trình sau :
a) \(2\sin^2x+\sin x\cos x-3\cos^2x=0\)
b) \(3\sin^2-4\sin x\cos x+5\cos^2x=2\)
c) \(\sin^2x+\sin2x-2\cos^2+5\cos^2x=2\)
d) \(2\cos^2x-3\sqrt{3}\sin2x-4\sin^2x=-4\)
a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; ![]() }.
}.
Vậy ![]()
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan3 + kπ, k ∈ Z.
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; ![]() =
= ![]() (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
(sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
![]() sin2x + 2sinxcosx -
sin2x + 2sinxcosx - ![]() cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan(-5) + kπ, k ∈ Z.
+ kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔