Bài 4 :Cho ABC vuông tại A kẻ AH BC tại H:a)Tìm các góc phụ nhaub)Chứng minh: ;
Đọc tiếp
Bài 4 : Cho a)Tìm các góc phụ nhau b)Chứng minh: |
|
HS
ABC vuông tại A kẻ AH 
BC tại H:
;
Những câu hỏi liên quan
Cho tam giác ABC cân tại A (góc A nhọn). Vẽ đường phân giác của góc BAC cắt BC tại H:a) Chứng minh HBHC VÀ AH vuông góc BC.b) Với AB30 cm, BC 36 cm.Tính độ dài AH.c) Vể đường trung tuyến BM của tam giác ABC cắt AH tại G.Tính độ dài AG và BM. A B C H G M 1 2
Đọc tiếp
Cho tam giác ABC cân tại A (góc A nhọn). Vẽ đường phân giác của góc BAC cắt BC tại H:
a) Chứng minh HB=HC VÀ AH vuông góc BC.
b) Với AB=30 cm, BC= 36 cm.Tính độ dài AH.
c) Vể đường trung tuyến BM của tam giác ABC cắt AH tại G.Tính độ dài AG và BM.
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC).
Tìm các cặp góc phụ nhau trong hình vẽ.
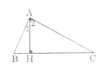
Tam giác ABC vuông tại A nên
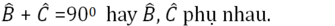
Tam giác AHB vuông tại H nên
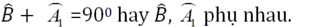
Tam giác AHC vuông tại H nên
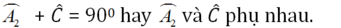
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.a)Chứng minh: ΔAHB ΔAHC.b)Chứng minh: HB HC và góc BAH góc CAHc)Kẻ HK vuông góc với AB tại K và HI vuông góc với AC tại I. Chứng minh: ΔHKB ΔHIC.Bài 2: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D.Kẻ DK⊥AB tại K.a)Chứng minh ΔABDΔKBD.b)Tia KD cắt tia BA tại M. Chứng minh AMKC và ΔBMC cân.c)Chứng minh AK // MC.Chứng minh BD⊥MC.
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.
a)Chứng minh: ΔAHB = ΔAHC.
b)Chứng minh: HB = HC và góc BAH = góc CAH
c)Kẻ HK vuông góc với AB tại K và HI vuông góc với AC tại I.
Chứng minh: ΔHKB = ΔHIC.
Bài 2: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D.
Kẻ DK⊥AB tại K.
a)Chứng minh ΔABD=ΔKBD.
b)Tia KD cắt tia BA tại M. Chứng minh AM=KC và ΔBMC cân.
c)Chứng minh AK // MC.
Chứng minh BD⊥MC.
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔABH=ΔACH
nên HB=HC và \(\widehat{BAH}=\widehat{CAH}\)
c: Xét ΔHKB vuông tại K và ΔHIC vuông tại I có
HB=HC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔHKB=ΔHIC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Kẻ đường cao AH( H thuộc BC)
a) Chứng minh tam giác ABC và tam giác HBA đồng dạng với nhau
b) Cho AB = 6cm, BC = 10cm. Tính HB
Bài 4. Cho tam giác ABC vuông tại A. Biết AB = 3cm, BC = 5cm.
a) Tính AC ?
b) Kẻ phân giác BD. Kẻ AH vuông góc BD tại H. Kéo dài AH cắt BC tại E. Chứng minh rằng: ▲ ABH =▲EBH .
c) Chứng minh rằng : DE ϵBC
d) Hai đường thẳng AB và DE cắt nhau tại K.Chứng minh rằng tam giác BCK cân
a: AC=4cm
b: Xét ΔABH vuông tại H và ΔEBH vuông tại H có
BH chung
\(\widehat{ABH}=\widehat{EBH}\)
Do đó: ΔABH=ΔEBH
c: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó:ΔBAD=ΔBED
Suy ra: \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE\(\perp\)BC
d: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra AK=EC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE
và AK=EC
nên BK=BC
=>ΔBKC cân tại B
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 4: Cho tam giác ABC vuông tại A (AB < AC). Kẻ AH vuông góc
với BC tại H. Phân giác của góc HAC cắt BC tại D. Hạ DE vuông góc
với AC tại E.
1. Chứng minh tam giác AHD = tam giác AED
2. Chứng minh góc BAD = góc BDA từ đó xác định dạng tam giác
ABD
3. Nếu tam giác AHE là tam giác đều thì tam giác ABD là tam
giác gì? Vì sao?
Giúp mình với ạ
1: Xét ΔAHD vuông tại H có ΔAED vuông tại E có
AD chung
\(\widehat{HAD}=\widehat{EAD}\)
Do đó; ΔAHD=ΔAED
2: Ta có: \(\widehat{BAD}+\widehat{CAD}=90^0\)
\(\widehat{BDA}+\widehat{HAD}=90^0\)
mà \(\widehat{HAD}=\widehat{CAD}\)
nên \(\widehat{BAD}=\widehat{BDA}\)
hay ΔBAD cân tại B
Đúng 0
Bình luận (0)
Bài 4: Cho tam giác ABC vuông tại A có 0 60B = , BM là tia phân giác của B ( ) M AC , từ M kẻ MN vuông góc với BC ( ) N BC a) Chứng minh ABM NBM = . b) Chứng minh NC AM . c) Từ A kẻ AH vuông góc với BC ( ) H BC , gọi I là giao điểm của AH và BM. Chứng minh tam giác AIM là tam giác đều.
a: Xét ΔBAM vuông tại A và ΔBNM vuông tại N có
BM chung
góc ABM=góc NBM
=>ΔBAM=ΔBNM
c:
góc HAC=90 độ-góc C
=90 độ-30 độ=60 độ
=>góc IAM=60 độ
góc AIM=góc BIH=90 độ-góc MBC
góc AMI=90 độ-góc ABM
mà góc MBC=góc ABM
nên góc AIM=góc AMI
=>ΔAMI cân tại A
mà góc IAM=60 độ
nên ΔAMI đều
Đúng 0
Bình luận (0)
Bài 4: Cho tam giác ABC vuông tại A đường cao AH . a) Chứng minh tam giác AHB đồng dạng tam giác ABC b) Gọi M , N lần lượt là trung điểm của BC và AB . Đường vuông góc BC kẻ từ B cắt MN tại I . Chứng minh c) IC cắt AH tại O . Chứng minh O là trung điểm AH d) Gọi K là giao điểm của CA và BI . Tính độ dài BK ,biết AB 15 cm , AC 20 cm .
Đọc tiếp
Bài 4: Cho tam giác ABC vuông tại A đường cao AH .
a) Chứng minh tam giác AHB đồng dạng tam giác ABC
b) Gọi M , N lần lượt là trung điểm của BC và AB . Đường vuông góc BC kẻ từ B cắt MN tại I . Chứng minh
c) IC cắt AH tại O . Chứng minh O là trung điểm AH
d) Gọi K là giao điểm của CA và BI . Tính độ dài BK ,biết AB = 15 cm , AC = 20 cm .
a. xét tam giác AHB và tam giác ABC có:
góc H= góc A=90o
góc B chung
-> tam giác AHB~tam giác ABC (g.g)
b. thiếu đề rồi bạn.
Đúng 2
Bình luận (1)
Cho▵ABC cân tại A. Kẻ tia AH vuông góc với BC ( H thuộc BC)
a) Chứng minh▵AHB =▵AHC
b) Chứng minh HB = HC
c) Kẻ IH vuông góc với AB tại I, HK vuông góc với AC tại K. Chứng minh▵AIK là tam giác cân d) Chứng minh IK // BC e) Chứng minh AH là đường trung trực của đoạn thẳng IK
a) Ta xét ▵AHB và▵AHC, ta có
AH là cạnh chung
AC=AB ( vì tam giác cân tại A)
góc AHC = góc AHB là góc vuông (90 độ)
-> ▵AHB =▵AHC (cạnh huyền- cạnh góc vuông)
b) Ta có ▵AHB =▵AHC (cmt)
->HB=HC ( 2 cạnh tương ứng)
c) Ta xét ▵AKH và ▵AIH. Ta có:
AH là cạnh chung
góc AKH = góc AIK = 90 độ
-> ▵AKH =▵AIH (cạnh huyền - cạnh góc vuông)
-> AK = AI (2 cạnh tương ứng) nên ▵AIK là tam giác cân và cân tại A
d) Ta áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Ta có AH là cạnh chung cùng vuông góc với IK và BC
-> IK // BC
e) Ta cho giao điểm của AH và IK là O
Ta xét ▵AKO và ▵AIO
Ta có AK=AI (cmt)
Góc AOK = góc AOI = 90 độ
-> ▵AKO = ▵AIO
-> KO = IO ( 2 cạnh tương ứng) -> AH là đường trung trực của đoạn thẳng IK
Đúng 2
Bình luận (0)