Cho hai số phức z 1 = a + 8 b + 20 i 3 , z 2 = 9 b - 4 - 10 a i Để z 1 , z 2 là liên hợp của nhau thì
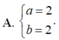
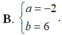
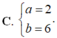

Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Gọi S là tập hợp tất cả các số phức z sao cho số phức w = \(\dfrac{1}{\left|z\right|-z}\)có phần thực bằng \(\dfrac{1}{8}\). Xét các số phức z1, z2 ϵ S thỏa mãn |z1-z2| = 2, giá trị lớn nhất của P = |z1 - 5i|2 - |z2 - 5i|2 bằng?
A. 16 B. 20 C. 10 D. 32
Giải thích chi tiết cho mình với ạ, mình cảm ơn nhiều
Đặt \(z=x+yi\Rightarrow w=\dfrac{1}{\sqrt{x^2+y^2}-x-yi}=\dfrac{\sqrt{x^2+y^2}-x+yi}{\left(\sqrt{x^2+y^2}-x\right)^2+y^2}\)
\(\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{\left(\sqrt{x^2+y^2}-x\right)^2+y^2}=\dfrac{1}{8}\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{2x^2+2y^2-2x\sqrt{x^2+y^2}}=\dfrac{1}{8}\)
\(\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{\sqrt{x^2+y^2}\left(\sqrt{x^2+y^2}-x\right)}=\dfrac{1}{4}\Rightarrow\dfrac{1}{\sqrt{x^2+y^2}}=\dfrac{1}{4}\)
\(\Rightarrow x^2+y^2=16\)
\(\Rightarrow\) Tập hợp \(z_1;z_2\) là đường tròn tâm O bán kính \(R=4\)
Gọi M, N lần lượt là điểm biểu diễn \(z_1;z_2\), do \(\left|z_1-z_2\right|=2\Rightarrow MN=2\)
Gọi \(P\left(0;5\right)\) và Q là trung điểm MN
\(\Rightarrow P=MP^2-NP^2=\overrightarrow{MP}^2-\overrightarrow{NP}^2=\left(\overrightarrow{MP}-\overrightarrow{NP}\right)\left(\overrightarrow{MP}+\overrightarrow{NP}\right)\)
\(=2\overrightarrow{MN}.\overrightarrow{PQ}=2\overrightarrow{MN}\left(\overrightarrow{PO}+\overrightarrow{OQ}\right)=2\overrightarrow{MN}.\overrightarrow{PO}=2MN.PO.cos\alpha\)
Trong đó \(\alpha\) là góc giữa \(MN;PO\)
Do MN, PO có độ dài cố định \(\Rightarrow P_{max}\) khi \(cos\alpha_{max}\Rightarrow\alpha=0^0\Rightarrow MN||PO\)
Mà MN=2 \(\Rightarrow M\left(\sqrt{15};-1\right);N\left(\sqrt{15};1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{PM}=\left(\sqrt{15};-6\right)\\\overrightarrow{PN}=\left(\sqrt{15};-4\right)\end{matrix}\right.\)
\(\Rightarrow P_{max}=PM^2-PN^2=15+36-\left(15+16\right)=20\)
Giúp e bài này với. Cho số phức z=a+bi sao cho (z-4)/(z-4i) là số thuần ảo. Nếu số phức có môdun lớn nhất thì biểu thức P= a2 + b2 bằng
A.4 B.8 C.24 D.20
\(z\ne4i\Rightarrow\left\{{}\begin{matrix}a\ne0\\b\ne4\end{matrix}\right.\)
\(\frac{z-4}{z-4i}=\frac{a-4+bi}{a+\left(b-4\right)i}=\frac{\left(a-4+bi\right)\left(a-\left(b-4\right)i\right)}{a^2-\left(b-4\right)^2}=\frac{a\left(a-4\right)+b\left(b-4\right)-\left[\left(a-4\right)\left(b-4\right)-ab\right]i}{a^2-\left(b-4\right)^2}\)
Số phức trên là thuần ảo khi và chỉ khi \(\left\{{}\begin{matrix}a\left(a-4\right)+b\left(b-4\right)=0\\\left(a-4\right)\left(b-4\right)-ab\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-2\right)^2+\left(b-2\right)^2=8\\a+b-4\ne0\end{matrix}\right.\)
\(\Rightarrow\) Tập hợp \(z\) là điểm \(M\left(a;b\right)\) thuộc đường tròn (C) tâm \(I\left(2;2\right)\) bán kính \(R=2\sqrt{2}\) và khác 2 điểm \(A\left(0;4\right)\) và \(B\left(4;0\right)\)
\(P=\left|z\right|^2=a^2+b^2=OM^2\)
\(P_{max}\) khi M trùng giao điểm của đường thẳng OI và đường tròn (giao điểm năm khác phía O so với I)
Phương trình OI: \(1\left(x-2\right)-1\left(y-2\right)=0\Leftrightarrow x-y=0\)
Giao điểm của OI và (C): \(2\left(x-2\right)^2=8\Rightarrow\left(x-2\right)^2=4\Rightarrow\left[{}\begin{matrix}x=4\\x=0\end{matrix}\right.\)
\(\Rightarrow M_1\left(0;0\right)\) (loại); \(M_2\left(4;4\right)\) \(\Rightarrow a=b=4\)
Không có kết quả?!
Cho hai số phức z = a + bi; a,b. Có điểm biểu diễn của số phức z nằm trong dải (-2;2) (hình 1) điều kiện của a và b là:
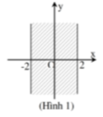
A. a ≥ 2 b ≥ 2
B. a ≤ - 2 b ≤ - 2
C. -2 < a < 2, b ∈ ℝ
D. a,b ∈ (-2;2)
Đáp án C
- Nhìn vào hình vẽ ta có phần thực a bị giới hạn -2 < a < 2, b ∈ ℝ
Chú ý: Cho số phức z = a + bi, điểm M(a;b) trong hệ trục tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z.
Cho hai số phức:
z = a + b i , z ' = a ' + b ' i ( a , b , a ' , b ' ∈ ℝ ) .
Tìm phần ảo của số phức z z ' .
A. ( a b ' + a ' b ) i
B. a b ' + a ' b
C. a b ' − a ' b
D. a a ' − b b '
Đáp án A.
Có z . z ' = a a ' − b b ' + a b ' + a ' b i .
Vậy phần ảo là: a b ' + b a ' i .
Cho hai số phức z = a + b i , z ' = a ' + b ' i ( a , b , a ' , b ' ∈ ℝ )
Tìm phần ảo của số phức z z ' .
A. ( a b ' + a ' b ) i
B. a b ' + a ' b
C. a b ' - a ' b
D. a a ' - b b '
Đáp án A.
Có ![]() .
.
Vậy phần ảo là (ab'+ba')i.
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và (1+i)z.
Tính z biết diện tích tam giác OAB bằng 8.
A. z = 2 2
B. z = 4 2
C. z = 2
D. z = 4
Đáp án D
HD: Ta có
![]()
Suy ra ∆OAB vuông cân tại A
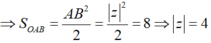
Cho hai số phức z = a + b i và z ' = a ' + b ' i ( a , b , a ' , b ' ∈ R ) Số phức z z ' có phần thực là
![]()
![]()
![]()
![]()
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và 1 + i z . Tính z biết diện tích tam giác OAB bằng 8.
A. z = 2 2 .
B. z = 4 2
C. z = 2
D. z = 4
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng (Oxy) biểu diễn các số phức z và 1 + i z . Tính |z| biết diện tích tam giác OAB bằng 8
A. z = 2 2
B. z = 4 2
C. z = 2
D. z = 4
Cho hai số phức z = a + b i và z ’ = a ’ + b ’ i (a,b,a’,b’ÎR) . Số phức zz’ có phần thực là
A. aa’ + bb’
B. ab’ – a’b
C. aa’ - bb’
D. ab’ + a’b