Giải bất phương trình 2017 - x 2016 + 2016 - x 2017 ≤ 1 . Gọi tập nghiệm là S. Tìm S
A. 2016 ; 2017
B. ( - ∞ , 2016 ] ∪ [ 2017 , + ∞ )
C. 2016 , 2017
D. S=R
Cho hàm số f ( x ) = x 3 - 3 x + 2018 . Tập nghiệm của bất phương trình f'(x) > 0 là:
A. (-1;1)
B. [-1;1]
C. - ∞ ; - 1 ∪ 1 ; + ∞
D. ( - ∞ ; - 1 ] ∪ [ 1 ; + ∞ )
Đáp án C.
- Phương pháp:
+) Tính f'(x).
+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.
- Cách giải:
+ Ta có:
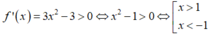
→ Vậy tập nghiệm của bất phương trình là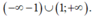 
1) Tìm tập nghiệm S của bất phương trình | 2x+1| > x+1
2) Tìm tất cả giá trị của tham số m để bất phương trình -x^2+x-m>0 vô nghiệm
2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
Cho bất phương trình: (x+2m)(x+1)>0. Tìm m để tập nghiệm của bất phương trình chứa (1;+∞)
- Với \(m=\dfrac{1}{2}\Rightarrow\left(x+1\right)^2>0\) có tập nghiệm \(R\backslash\left\{-1\right\}\) thỏa mãn
- Với \(m>\dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-1\\x< -2m\end{matrix}\right.\) hay \(D=\left(-\infty;-2m\right)\cup\left(-1;+\infty\right)\)
Thỏa mãn do \(\left(1;+\infty\right)\subset\left(-1;+\infty\right)\)
- Với \(m< \dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-2m\\x< -1\end{matrix}\right.\) hay \(D=\left(-\infty;-1\right)\cup\left(-2m;+\infty\right)\)
Tập nghiệm của BPT chứa \(\left(1;+\infty\right)\) khi:
\(-2m\le1\Rightarrow m\ge-\dfrac{1}{2}\Rightarrow-\dfrac{1}{2}\le m< \dfrac{1}{2}\)
Kết hợp lại ta được: \(m\ge-\dfrac{1}{2}\)
Bài 3 :Cho bất phương trình : 3x(2x + 5) x(6x -1) + 4
a) Giải bất phương trình và biểu diễn tập nghiệm trên trục số.
b) Tìm nghiệm nguyên nhỏnhất của bất phương trình trên.
Tìm tập nghiệm của bất phương trình 2017 2018 x − 1 > 2017 2018 − x + 3 .
A. 2 ; + ∞ .
B. − ∞ ; 2 .
C. 2 ; + ∞ .
D. − ∞ ; 2 .
Tìm tập nghiệm của bất phương trình log 2 5 ( x - 4 ) + 1 > 0 .
A. [ 13 2 ; + ∞ )
B. - ∞ ; 13 2
C. 4 ; + ∞
D. 4 ; 13 2
Tìm tập nghiệm S của bất phương trình log 0 , 2 x − 1 < log 0 , 2 3 − x .
A. S = − ∞ ; 3
B. S = 2 ; 3
C. S = 2 ; + ∞
D. S = 1 ; 2
Đáp án B
B P T ⇔ 1 < x < 3 x 01 > 3 − x ⇔ 1 < x < 3 x > 2 ⇔ 2 < x < 3.
Tìm tập nghiệm S của bất phương trình log 2 x + 1 < log 2 3 - x
A. S = - ∞ ; 1
B. S = 1 ; + ∞
C. S = (1;3]
D. S = (-1;1)
Tìm tập nghiệm S của bất phương trình log 0 , 2 x − 1 < log 0 , 2 3 − x .
A. S = − ∞ ; 3
B. S = (2;3)
C. S = 2 ; + ∞
D. S = (1;2)
