Tính theo a thể tích của khối lăng trụ đứng A B C D . A ’ B ’ C ’ D ’ có đáy là hình thoi cạnh a, góc BAD bằng 60 ° và cạnh bên AA’ bằng a.
A. 9 2 a 3
B. 1 2 a 3
C. 3 2 a 3
D. 3 4 a 3
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, biết A'B tạo với đáy một góc 300 và AB = 2a, AD = 4a. Tính thể tích khối lăng trụ đã cho theo a.
\(AA'=\dfrac{2a}{\sqrt{3}}\)
\(V=AA'\cdot S_{ABCD}=\dfrac{16a^3}{\sqrt{3}}\)
Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là hình vuông cạnh bằng 4cm, đường chéo AB′ của mặt bên (ABB′A′) có độ dài bằng 5cm. Tính thể tích V của khối lăng trụ ABCD.A′B′C′D′.
A. 48 cm 3
B. 24 cm 3
C. 16 cm 3
D. 32 cm 3
Cho lăng truh đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, biết A'B tạo với đáy một góc 300 và AB = 2a, AD = 4a. Tính thể tích khối lăng trụ đã cho theo a.
Cho khối lăng trụ đứng ABCD.A'B'C'D' có đáy là hình vương, cạnh đáy bằng \(2a\sqrt{2}\) và đường chéo AC'=5a. Tính thể tích khối lăng trụ đã cho
A. \(24a^3\) B. \(8a^3\) C.\(17\sqrt{2}a^3\) D.\(4a^3\)
\(AC=AB\sqrt{2}=4a\)
Áp dụng định lý Pitago:
\(CC'=\sqrt{\left(AC'\right)^2-AC^2}=3a\)
\(\Rightarrow V=3a.\left(2a\sqrt{2}\right)^2=24a^3\)
Cho hình lăng trụ đứng ABC.A' B' C' có đáy ABC là tam giác vuông tại A, biết AB = a, AC = 2a và A' B = 3a. Tính thể tích của khối lăng trụ ABC.A' B' C'.
A. 2 2 a 3
B. 5 a 3 3
C. 2 2 a 3 3
D. 5 a 3
Chọn A.
Phương pháp
Tính diện tích tam giác đáy và chiều cao lăng trụ suy ra thể tích theo công thức V=Bh .
Cách giải:
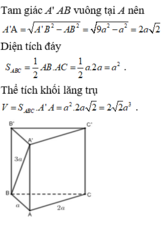
Cho hình lăng trụ đứng ABC.A' B' C' có đáy ABC là tam giác vuông tại A, biết AB = a, AC = 2a và A' B = 3a. Tính thể tích của khối lăng trụ ABC.A' B' C'.
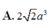
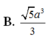
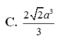
![]()
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi, cạnh a; \(\widehat{BAD}=60^0\). Biết \(AB'\perp BD'\). Tính thể tích khối lăng trụ \(\left(V=S_đ.h\right)\)
Đặt \(x=AA'\)
Ta có: \(\overrightarrow{AB'}=\overrightarrow{AA'}+\overrightarrow{AB}\) ; \(\overrightarrow{BD'}=\overrightarrow{BB'}+\overrightarrow{BD}=\overrightarrow{BB'}+\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AB'}.\overrightarrow{BD'}=\left(\overrightarrow{AA'}+\overrightarrow{AB}\right)\left(\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=AA'^2+\overrightarrow{AA'}\left(-\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}.\overrightarrow{AA'}-AB^2+\overrightarrow{AB}.\overrightarrow{BC}\)
\(=x^2-a^2+AB.BC.cos120^0\)
\(=x^2-a^2-\dfrac{a^2}{2}=x^2-\dfrac{3a^2}{2}=0\)
\(\Rightarrow x=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{a\sqrt{6}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{2}}{4}\)
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác đều cạnh a. Cạnh bên BB′=b. Thể tích của khối lăng trụ ABC.A′B′C′ là
A. a 3 b 3
B. a 2 b 3 4
C. a 2 b 3
D. a 3 b 3 3
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình vuông cạnh a. Tính thể tích V của khối lăng trụ đã cho theo a, biết A'B = 2a.
A. V = 2 3 a 3
B. V = a3
C. V = 3 a 3
D. V = 3 a 3 3
Đáp án C
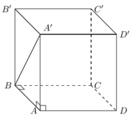
Diện tích đáy lăng trụ là a2.
Chiều cao của lăng trụ là A A ' = A ' B 2 - B A 2 = 4 a 2 - a 2 = a 3
Vậy thể tích lăng trụ là V = √3a3
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
\(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.a.a\sqrt{3}=\dfrac{a^2\sqrt{3}}{2}\)
\(\Rightarrow V_{ABC}.A'B'C'=AA'.S_{ABC}=2a.\dfrac{a^2\sqrt{3}}{2}=a^3\sqrt{3}\)
Chọn A