Cho hàm số y = x - 2 x + 1 . Viết phương trình tiếp tuyến của đồ thị hàm số trên tại điểm có hoành độ x 0 = 0
A. y = 3 x - 2
B. y = - 3 x - 2
C. y = 3 x - 3
D. y = 3 x + 2
Cho hàm số: \(y=\dfrac{x-1}{x+1}\) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: \(y=\dfrac{x-2}{2}\)
Ta có : \(y=\dfrac{x-1}{x+1}\Rightarrow y'=\dfrac{\left(x+1\right)-\left(x-1\right)}{\left(x+1\right)^2}=\dfrac{2}{\left(x+1\right)^2}\)
Giả sử d' là tiếp tuyến của đths đã cho . Do d' // d : y = \(\dfrac{x-2}{2}\)
\(\Rightarrow d'\) có HSG = 1/2 \(\Rightarrow\dfrac{2}{\left(x+1\right)^2}=\dfrac{1}{2}\Leftrightarrow4=\left(x+1\right)^2\) \(\Leftrightarrow\left[{}\begin{matrix}x+1=2\\x+1=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Với x = 1 . PTTT d' : \(y=\dfrac{1}{2}\left(x-1\right)+0=\dfrac{1}{2}x-\dfrac{1}{2}\)
Với x = -3 . PTTT d' : \(y=\dfrac{1}{2}\left(x+3\right)+2=\dfrac{1}{2}x+\dfrac{7}{2}\)
Cho hàm số: \(y=\dfrac{x-1}{x+1}\) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: \(y=\dfrac{x-2}{2}\)
y'=(x-1)'(x+1)-(x-1)(x+1)'/(x+1)^2=(x+1-x+1)/(x+1)^2=2/(x+1)^2
(d1)//(d)
=>(d1): y=1/2x+b
=>y'=1/2
=>(x+1)^2=4
=>x=1 hoặc x=-3
Khi x=1 thì f(1)=0
y-f(1)=f'(1)(x-1)
=>y-0=1/2(x-1)=1/2x-1/2
Khi x=-3 thì f(-3)=(-4)/(-2)=2
y-f(-3)=f'(-3)(x+3)
=>y-2=1/2(x+3)
=>y=1/2x+3/2+2=1/2x+7/2
Cho hàm số y = x - 1 x + 1 . Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = – 2.
Cho hàm số y=f(x) có đạo hàm liên tục trên R và thỏa mãn 2f(5-3x)+3f(x+1)=x^2+4x+5. Viết phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ bằng 2
Thay \(x=1\Rightarrow2f\left(2\right)+3f\left(2\right)=10\Rightarrow f\left(2\right)=5\)
Đạo hàm 2 vế giả thiết:
\(-6f'\left(5-3x\right)+3f'\left(x+1\right)=2x+4\)
Thay \(x=1\)
\(-6f'\left(2\right)+3f'\left(2\right)=6\Rightarrow f'\left(2\right)=-2\)
Phương trình tiếp tuyến:
\(y=-2\left(x-2\right)+5=-2x+9\)
(1 điểm)
Cho hàm số $y=x^3-3x^2+2$. Viết phương trình tiếp tuyến với đồ thị hàm số biết hoành độ tiếp điểm bằng $-1$.
Y=9x+7
https://drive.google.com/file/d/14Q-YI3szy-rePnIHWGD35RKCWiCXCT6k/view?usp=sharing
Cho hàm số y = x - 1 x + 1 . Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d : y = x - 2 2
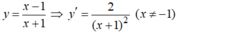
d: 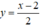 có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
- Gọi ( x 0 , y 0 ) là toạ độ của tiếp điểm.
- Ta có:
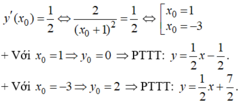
Cho hàm số \(y=f\left(x\right)\) xác định và có đạo hàm trên R thỏa mãn: \(\left[f\left(1+2x\right)\right]^3=8x-\left[f\left(1-x\right)\right]^2\), ∀x∈R. viết phương trình tiếp tuyến của đồ thị hàm số \(y=f\left(x\right)\) tại điểm có hoành độ bằng 1.
I. Cho hàm số y = x3 - 2x2 + x - 1 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị hàm số (C), biết rằng đồ thị này song song với đường thẳng y = -5x + 17.
II. Xét tính liên tục của hàm số sau:
\(\left\{{}\begin{matrix}\dfrac{-x^2+2x+1}{-x-1}|khix=-1\\3-2x|khix=1\end{matrix}\right.\)tại x0 = 1
III. Cho hình chóp S.ABCD có SA \(\perp\) (ABCD), ABCD là hình chữ nhật. Chứng minh rằng BC \(\perp\) (SAC).
Giải giúp mình nhé. Mai mình thi HKII rồi. Cảm ơn các bạn rất nhiều.
Đề số 2:
Bài tập 1: Cho hàm số y = \(\dfrac{3x+1}{x+2}\)
a, Khảo sát
b, Viết phương trình tiệp tuyến của (C) tại điểm có x = -1
a.
TXĐ: \(D=R\backslash\left\{-2\right\}\)
Sự biến thiên: \(y'=\dfrac{5}{\left(x+2\right)^2}>0\) ; \(\forall x\ne-2\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-2\right)\) và \(\left(-2;+\infty\right)\)
\(\lim\limits_{x\rightarrow-2}\dfrac{3x+1}{x+2}=\infty\Rightarrow x=-2\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow\infty}\dfrac{3x+1}{x+2}=3\Rightarrow y=3\) là tiệm cận ngang
Bảng biến thiên:
b.
\(y'\left(-1\right)=\dfrac{5}{\left(-1+2\right)^2}=5\) ; \(y\left(-1\right)=\dfrac{3.\left(-1\right)+1}{-1+2}=-2\)
Phương trình tiếp tuyến:
\(y=5\left(x+1\right)-2\Leftrightarrow y=5x+3\)
Cho hàm số y= f(x) xác định và có đạo hàm trên ℝ thỏa mãn f 1 + 2 x 2 = x - f 1 - x 3 . Viết phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ bằng 1.
A. y = - 1 7 x - 6 7
B. y = 1 7 x - 8 7
C. y = - 1 7 x + 8 7
D. y = - x + 6 7
Đáp án A
Đặt f 1 = a f ' 1 = b , thay x = 0 vào giả thiết, ta được f 2 1 = - f 3 0 ⇔ a 3 + a 2 = 0 ⇔ [ a = 0 a = - 1
Đạo hàm cả 2 vế biểu thức f 2 1 + 2 x = x - f 3 1 - x , ta đưuọc
4 f ' 1 + 2 x . f 1 + 2 x = 1 + 3 f ' 1 - x . f 2 1 - x 1
Thay x = 0 vào (1), ta có 4 f ' 1 . f 1 = 1 + 3 f ' 1 . f 2 1 ⇔ 4 a b = 1 + 3 a 2 b 2
TH1. Với a = 0 thay vào (2), ta được 0 = 1 (vô lí)
TH2. Với a = -1 thay vào (2), ta được - 4 b = 1 + 3 b ⇔ b = - 1 7 ⇒ f ' 1 = - 1 7
Vậy phương trình tiếp tuyến cần tìm là y - f 1 = f ' 1 x - 1 ⇒ y = - 1 7 x - 6 7 .