Giải phương trình sau: tan x - c o t x = 3 2
![]()
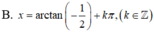
![]()
![]()
1/ Giải phương trình sau:
\(tan^2\left(x+\dfrac{\pi}{3}\right)+\left(\sqrt{3}-1\right)tan\left(x+\dfrac{\pi}{3}\right)-\sqrt{3}=0\)
Đặt \(tan\left(x+\dfrac{\pi}{3}\right)=t\)
\(\Rightarrow t^2+\left(\sqrt{3}-1\right)t-\sqrt{3}=0\)
\(\Leftrightarrow t\left(t-1\right)+\sqrt{3}\left(t-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}t=1\\t=-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tan\left(x+\dfrac{\pi}{3}\right)=1\\tan\left(x+\dfrac{\pi}{3}\right)=-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{4}+k\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k\pi\\x=-\dfrac{2\pi}{3}+k\pi\end{matrix}\right.\)
Giải các phương trình sau :
a) \(2\tan x-3\cot x-2=0\)
b) \(\cos^2=3\sin2x+3\)
c) \(\cot x-\cot2x=\tan x+1\)
1/ Giải phương trình sau:
\(tan^2\left(x+\dfrac{\pi}{3}\right)+\left(\sqrt{3}-1\right)tan\left(x+\dfrac{\pi}{3}\right)-\sqrt{3}=0\)
2/ Tìm hệ số của số hạng chứa \(x^{26}\) trong khai triển \(\left(\dfrac{1}{x^4}+x^7\right)^n\) . Biết \(C^2_{n+2}-4C^n_{n+1}=2\left(n+1\right)\) (n ∈ N* ; x > 0)
Câu 2:
\(\Leftrightarrow\dfrac{\left(n+2\right)!}{2!\cdot n!}-4\cdot\dfrac{\left(n+1\right)!}{n!\cdot1!}=2\left(n+1\right)\)
\(\Leftrightarrow\dfrac{\left(n+1\right)\left(n+2\right)}{2}-4\cdot\dfrac{n+1}{1}=2\left(n+1\right)\)
\(\Leftrightarrow\left(n+1\right)\left(n+2\right)-8\left(n+1\right)=4\left(n+1\right)\)
=>(n+1)(n+2-8-4)=0
=>n=-1(loại) hoặc n=10
=>\(A=\left(\dfrac{1}{x^4}+x^7\right)^{10}\)
SHTQ là: \(C^k_{10}\cdot\left(\dfrac{1}{x^4}\right)^{10-k}\cdot x^{7k}=C^k_{10}\cdot1\cdot x^{11k-40}\)
Số hạng chứa x^26 tương ứng với 11k-40=26
=>k=6
=>Số hạng cần tìm là: \(210x^{26}\)
Giải phương trình sau :
\(2\tan^2x-3\tan x+2\cot^2x+3\cot x-3=0\)
Giải phương trình sau:
\(\tan\left(x+\dfrac{\pi}{3}\right)+\cot\left(\dfrac{\pi}{2}-3x\right)=0\)
Pt \(\Leftrightarrow\)\(tan\left(x+\dfrac{\pi}{3}\right)\)=\(-cot\left(\dfrac{\pi}{2}-3x\right)\)
\(\Leftrightarrow\)\(tan\left(x+\dfrac{\pi}{3}\right)\)=\(tan\left(\dfrac{\pi}{2}+\dfrac{\pi}{2}-3x\right)\)=\(tan\left(\pi-3x\right)\)
\(\Leftrightarrow\)\(x+\dfrac{\pi}{3}=\pi-3x+k\pi\)
\(\Leftrightarrow\)4\(x\)=\(\dfrac{4}{3}\pi+k\pi\)
\(\Leftrightarrow\) \(x=\) \(\dfrac{\pi}{3}+k\dfrac{\pi}{4}\)(\(k\in Z\))
\(pt\Leftrightarrow tan\left(x+\dfrac{\pi}{3}\right)=-cot\left(\dfrac{\pi}{2}-3x\right)\)
\(\Leftrightarrow tan\left(x+\dfrac{\pi}{3}\right)=cot\left(-\dfrac{\pi}{2}+3x\right)\)
\(\Leftrightarrow tan\left(x+\dfrac{\pi}{3}\right)=tan\left(\dfrac{\pi}{2}+\dfrac{\pi}{2}-3x\right)\)
\(\Leftrightarrow tan\left(x+\dfrac{\pi}{3}\right)=tan\left(\pi-3x\right)\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\pi-3x+k\pi\)
\(\Leftrightarrow4x=\dfrac{2\pi}{3}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{4}\)
giải phương trình sau : a) \(\tan\frac{x}{2}=\tan x\) ; b) \(\tan\left(2x+10^o\right)+\cot x=0\) ; c) \(\left(1-\tan x\right)\left(1+\sin2x\right)=1+\tan x\) ; d) \(\tan x+\tan2x=\sin3x\cos x\) ; e) \(\tan x+\cot2x=2\cot4x\)
giải phương trình sau : a) \(\tan\frac{x}{2}=\tan x\) ; b) \(\tan\left(2x+10^o\right)+\cot x=0\) ; c) \(\left(1-\tan x\right)\left(1+\sin2x\right)=1+\tan x\) ; d) \(\tan x+\tan2x=\sin3x\cos x\) ; e) \(\tan x+\cot2x=2\cot4x\)
Giải phương trình sau: tanx + tan (x+π/4) = 1
Điều kiện:
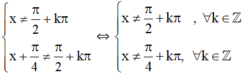
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2.tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx(tanx - 3) = 0
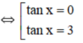
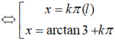
Vậy phương trình đã cho có tập nghiệm là:
{arctan 3+kπ; k ∈ Z }
Giải các Phương trình sau
a) \(sin^4\frac{x}{2}+cos^4\frac{x}{2}=\frac{1}{2}\)
b) \(sin^6x+cos^6x=\frac{7}{16}\)
c) \(sin^6x+cos^6x=cos^22x+\frac{1}{4}\)
d) \(tanx=1-cos2x\)
e) \(tan(2x+\frac\pi3).tan(\frac\pi3-x)=1\)
f) \(tan(x-15^o).cot(x+15^o)=\frac{1}{3}\)
a.
\(\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)^2-2sin^2\dfrac{x}{2}cos^2\dfrac{x}{2}=\dfrac{1}{2}\)
\(\Leftrightarrow2-\left(2sin\dfrac{x}{2}cos\dfrac{x}{2}\right)^2=1\)
\(\Leftrightarrow1-sin^2x=0\)
\(\Leftrightarrow cos^2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
b.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\dfrac{7}{16}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=\dfrac{7}{16}\)
\(\Leftrightarrow16-12.sin^22x=7\)
\(\Leftrightarrow3-4sin^22x=0\)
\(\Leftrightarrow3-2\left(1-cos4x\right)=0\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow4x=\pm\dfrac{2\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
c.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=cos^22x+\dfrac{1}{4}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=cos^22x+\dfrac{1}{4}\)
\(\Leftrightarrow3-3sin^22x=4cos^22x\)
\(\Leftrightarrow3=3\left(sin^22x+cos^22x\right)+cos^22x\)
\(\Leftrightarrow3=3+cos^22x\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)