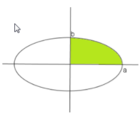
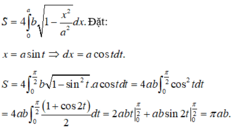Cho elip (E) có phương trình: x 2 100 + y 2 36 = 1
a, Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip (E) và vẽ elip đó.
b, Qua tiêu điểm của elip dựng đường song song với Oy và cắt elip tại hai điểm M và N. Tính độ dài đoạn MN.
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\). Tìm các tiêu điểm và tiêu cự của elip.
Ta có: \(c = \sqrt {{{100}^2} - {{64}^2}} = 6\). Do đó (E) có hai tiêu điểm là \({F_1}\left( { - 6;0} \right),{F_2}\left( {6;0} \right)\) và có tiêu cự bằng 2c = 12.
Cho Elip có phương trình \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\). Tìm tiêu điểm và tiêu cự của elip.
Ta có: \({a^2} = 36,{b^2} = 9 \Rightarrow c = \sqrt {36 - 9} = 3\sqrt 3 \) nên elip có hai tiêu điểm là \({F_1}\left( { - 3\sqrt 3 ;0} \right);{F_2}\left( {3\sqrt 3 ;0} \right)\) và tiêu cự là \({F_1}{F_2} = 2c = 6\sqrt 3 \).
a, cho elip (E) có phương trình chính tắc x^2/49+y^2/25=1. tìm toạ độ các giao điểm của (E) với các trục ox,oy và toạ độ các tiêu điểm của (E)
Cho elip \(\left( E \right)\) có phương trình chính tắc \(\frac{{{x^2}}}{{49}} + \frac{{{y^2}}}{{25}} = 1\) .Tìm tọa độ các giao điểm của \(\left( E \right)\) với trục Ox, Oy và tọa độ các tiêu điểm của \(\left( E \right)\).
Từ phương trình chính tắc của (E) ta có: \(a = 7,b = 5 \Rightarrow c = 2\sqrt 6 {\rm{ }}(do{\rm{ }}{{\rm{c}}^2} + {b^2} = {a^2})\)
Vậy ta có tọa độ các giao điểm của (E) với trục Ox, Oy là: \({A_1}\left( { - 7;{\rm{ }}0} \right)\)\({A_2}\left( {7;{\rm{ }}0} \right)\)\({B_1}\left( {0; - {\rm{ 5}}} \right)\)\({B_2}\left( {0;{\rm{ 5}}} \right)\)
Hai tiêu điểm của (E) có tọa độ là: \({F_1}\left( { - 2\sqrt 6 ;0} \right),{F_2}\left( {2\sqrt 6 ;0} \right)\)
Cho elip (E) có phương trình x²/16 + y²/9 =1. Viết phương trình đường thẳng (d) đi qua M(1;2) và cắt (E) tại A, B sao cho M là trung điểm AB
trong mặt phẳng với hệ tọa độ Oxy, cho elip(E) có phương trình chính tắc \(\dfrac{x^2}{169}+\dfrac{y^2}{25}=1\)
, với hai tiêu điểm là F1 và F2. Với điểm M bất kì trên (E) thì chu vi tam giác MF1F2 là
Chu vi: \(P=F_1F_2+MF_1+MF_2=2c+2a=2\sqrt{a^2-b^2}+2a=2\sqrt{169-25}+2.13=50\)
Cho elip (E) có phương trình x 2 m 2 + y 2 6 m = 1 . Giá trị của m để phương trình đó là phương trình chính tắc của một elip có tiêu cự bằng 8 là:
A. m = - 2
B. m = 8
C. m = - 2 hoặc m = 8
D. không tồn tại m
Trong mặt phẳng Oxy, cho elip \((E): \frac{x^2}{9}+\frac{y^2}{4}=1\). Tìm phương trình của (E') là ảnh của (E) qua phép tịnh tiến theo véctơ \(\overrightarrow{v}\) trong các trường hợp sau
a) \(\overrightarrow{v}=(4;-3)\)
b) \(\overrightarrow{v}=(2;1)\)
c) \(\overrightarrow{v}=(-2;1)\)
Cho a > b > 0 . Đường elip E có phương trình x 2 a 2 + y 2 b 2 = 1 . Diện tích của hình elip E là
A. πab
B. 4 πab
C. a 2 + b 2 2 π
D. 2 πab
Đáp án A
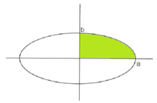
Xét hình phẳng D giới hạn bởi các trục Ox, Oy và đồ thị của hàm số 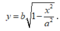
Diện tích elip bằng 4 lần diện tích hình phẳng D.
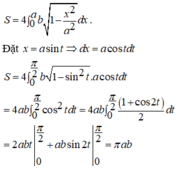
Cho a > b > 0 . Đường elip (E) có phương trình x 2 a 2 + y 2 b 2 = 1 . Diện tích của hình elip (E) là
A. a 2 + b 2 2 π
B. 2 πab
C. 4 πab
D. πab
Đáp án D
Xét hình phẳng D giới hạn bởi các trục Ox, Oy và đồ thị của hàm số y = b 1 − x 2 a 2 . Diện tích elip bằng 4 lần diện tích hình phẳng D.