Mng giúp em với ạ. Em cảm ơn!!!
NT
Những câu hỏi liên quan
 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5
Đúng 0
Bình luận (0)
Mng giúp em với ạ em cảm ơn 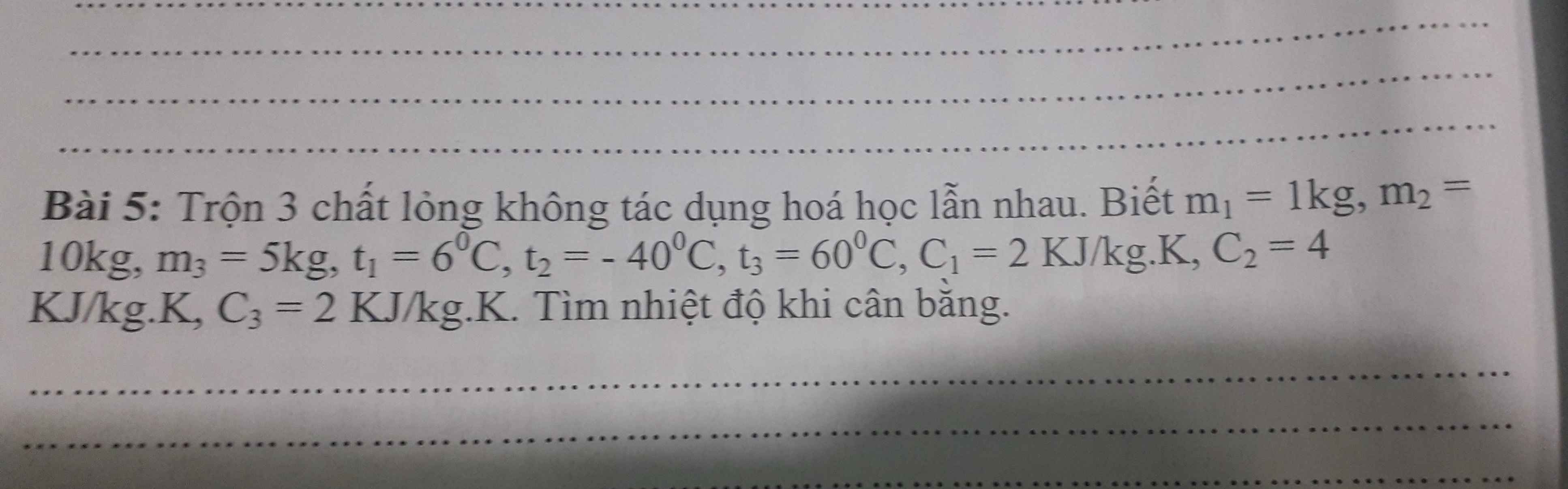
Gọi nhiệt độ cân bằng là \(t\left(t_2< t< t_3\right)\)
Giả sử \(t>t_1\Rightarrow Q_{thu}=Q_1+Q_2;Q_{tỏa}=Q_3\)
\(Q_{thu}=Q_{tỏa}\)
\(\Leftrightarrow Q_1+Q_2=Q_3\)
\(\Leftrightarrow m_1.C_1.\left(t-t_1\right)+m_2.C_2.\left(t-t_2\right)=m_3.C_3.\left(t_3-t\right)\)
\(\Leftrightarrow2000.\left(t-6\right)+10.4000.\left(t+40\right)=5.2000.\left(60-t\right)\)
\(\Leftrightarrow t=-19^oC\) (Trái với giả sử)
\(\Rightarrow t< t_1\Rightarrow Q_{thu}=Q_2;Q_{tỏa}=Q_1+Q_3\)
\(Q_{thu}=Q_{tỏa}\)
\(\Leftrightarrow m_2.C_2.\left(t-t_2\right)=m_1.C_1.\left(t-t_1\right)+m_3.C_3.\left(t_3-t\right)\)
\(\Leftrightarrow10.4000.\left(t+40\right)=2000.\left(t-6\right)+5.2000.\left(60-t\right)\)
\(\Leftrightarrow t=-19^oC\)
Kết luận: Nhiệt độ khi cân bằng là \(t=-19^oC\)
Đúng 0
Bình luận (0)
Giúp em với ạ em cảm ơn mng
\(\lim\limits_{x\rightarrow-\infty}\dfrac{3x^3-5x-6}{1-4x^3+x^2}=\lim\limits_{x\rightarrow-\infty}\dfrac{x^3\left(3-\dfrac{5}{x^2}-\dfrac{6}{x^3}\right)}{x^3\left(\dfrac{1}{x^3}-4+\dfrac{1}{x}\right)}=\lim\limits_{x\rightarrow-\infty}\dfrac{3-\dfrac{5}{x^2}-\dfrac{6}{x^3}}{\dfrac{1}{x^3}-4+\dfrac{1}{x}}=\dfrac{3-0-0}{0-4+0}=-\dfrac{3}{4}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(3x^2+8\right)\left(2x+1\right)}{5-4x^3}=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2\left(3+\dfrac{8}{x}\right)x\left(2+\dfrac{1}{x}\right)}{x^3\left(\dfrac{5}{x^3}-4\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(3+\dfrac{8}{x}\right)\left(2+\dfrac{1}{x}\right)}{\dfrac{5}{x^3}-4}=\dfrac{\left(3+0\right)\left(2+0\right)}{0-4}=-\dfrac{6}{4}=-\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{-5x+7}{3-2x}=\lim\limits_{x\rightarrow+\infty}\dfrac{x\left(-5+\dfrac{7}{x}\right)}{x\left(\dfrac{3}{x}-2\right)}=\lim\limits_{x\rightarrow+\infty}\dfrac{-5+\dfrac{7}{x}}{\dfrac{3}{x}-2}=\dfrac{-5+0}{0-2}=\dfrac{5}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{7}{2x-1}=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{7}{x}}{2-\dfrac{1}{x}}=\dfrac{0}{2-0}=0\)
Đúng 0
Bình luận (1)
Mng giúp em với ạ, em cảm ơn

a.
C là trung điểm của AD nên tọa độ D thỏa mãn:
\(\left\{{}\begin{matrix}x_D=2x_C-x_A=-3\\y_D=2y_C-y_A=3\\z_D=2z_C-z_A=4\end{matrix}\right.\) \(\Rightarrow D\left(-3;3;4\right)\)
b.
Gọi \(E\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3;0;-3\right)\\\overrightarrow{EC}=\left(-2-x;2-y;3-z\right)\end{matrix}\right.\)
ABCE là hbh \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{EC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2-x=3\\2-y=0\\3-z=-3\end{matrix}\right.\) \(\Leftrightarrow E\left(-5;2;6\right)\)
Đúng 0
Bình luận (0)
c.
Gọi \(F\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{FA}=\left(-1-x;1-y;2-z\right)\\\overrightarrow{FB}=\left(2-x;1-y;-1-z\right)\\\overrightarrow{FC}=\left(-2-x;2-y;3-z\right)\end{matrix}\right.\)
\(2\overrightarrow{FA}+3\overrightarrow{FB}=\overrightarrow{FC}\Leftrightarrow\left\{{}\begin{matrix}2\left(-1-x\right)+3\left(2-x\right)=-2-x\\2\left(1-y\right)+3\left(1-y\right)=2-y\\2\left(2-z\right)+3\left(-1-z\right)=3-z\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{3}{4}\\z=-\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow F\left(\dfrac{3}{2};\dfrac{3}{4};-\dfrac{1}{2}\right)\)
d.
Gọi G có tọa độ dạng: \(G\left(x;y;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AG}=\left(x+1;y-1;-2\right)\\\overrightarrow{BG}=\left(x-2;y-1;1\right)\end{matrix}\right.\)
Ba điểm A;B;G thẳng hàng khi:
\(\dfrac{x-2}{x+1}=\dfrac{y-1}{y-1}=\dfrac{1}{-2}\)
\(\Rightarrow\) Không tồn tại G thỏa mãn yêu cầu đề bài
Đúng 0
Bình luận (0)
e.
Gọi \(H\left(0;y;0\right)\) và H' là trọng tâm tam giác HBC
\(\Rightarrow H'\left(0;\dfrac{y+3}{3};\dfrac{2}{3}\right)\)
H' thuộc Oz khi và chỉ khi \(\dfrac{y+3}{3}=0\Leftrightarrow y=-3\)
\(\Rightarrow H\left(0;-3;0\right)\)
f.
\(\left\{{}\begin{matrix}S_{ABC}=\dfrac{1}{2}AB.d\left(C;AB\right)\\S_{ABI}=\dfrac{1}{2}AB.d\left(I;AB\right)\end{matrix}\right.\)
Mà \(S_{ABC}=3S_{ABI}\Rightarrow d\left(C;AB\right)=3d\left(I;AB\right)\)
\(\Rightarrow\overrightarrow{CB}=3\overrightarrow{IB}\)
Gọi \(I\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{CB}=\left(4;-1;-4\right)\\\overrightarrow{IB}=\left(2-x;1-y;-1-z\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3\left(2-x\right)=4\\3\left(1-y\right)=-1\\3\left(-1-z\right)=-4\end{matrix}\right.\) \(\Leftrightarrow...\) (bạn tự giải ra kết quả)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
 mng giải giúp em câu 10 với ạ, em cảm ơn ạ!
mng giải giúp em câu 10 với ạ, em cảm ơn ạ!
Câu 10:
Gọi \(H\) là giao điểm của \(MO\) và \(AB\).
Xét tam giác \(MAO\) vuông tại \(A\) đường cao \(AH\):
\(\dfrac{1}{AH^2}=\dfrac{1}{MA^2}+\dfrac{1}{AO^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{R\sqrt{2}}{2}\right)^2}=\dfrac{1}{MA^2}+\dfrac{1}{R^2}\Leftrightarrow MA=R\).
\(S_{MAOB}=S_{MAO}+S_{MBO}\)
\(=\dfrac{1}{2}.AO.MA+\dfrac{1}{2}.OB.MB\)
\(=\dfrac{1}{2}.R.R+\dfrac{1}{2}.R.R=R^2\)
Chọn C.
Đúng 2
Bình luận (0)
 mng giải giúp em câu 15 với ạ, em cảm ơn ạ!
mng giải giúp em câu 15 với ạ, em cảm ơn ạ!
Đài ơi, giải giúp cho Sarah đi, tớ không có viết và giờ vào giường rồi , good nigh
Đúng 0
Bình luận (0)
Mng giúp em với, em cảm ơn nhiều ạ
Câu 28: C
Câu 27: D
Câu 26: C
Câu 25: B
Đúng 1
Bình luận (0)
Mng giúp em 4 câu này với ạ, em cảm ơn ạ😭
\(Cu\left(OH\right)_2+2HNO_3\rightarrow Cu\left(NO_3\right)_2+2H_2O\\ MgO+2HCl\rightarrow MgCl_2+H_2O\\ Fe\left(OH\right)_3+3HCl\rightarrow FeCl_3+3H_2O\\ Fe_2\left(SO_4\right)_3+3BaCl_2\rightarrow3BaSO_4\downarrow+2FeCl_3\)
Đúng 2
Bình luận (0)
Mng giúp em bài này với ạ em cảm ơn !
Đọc tiếp
 Mng giúp em bài này với ạ
Mng giúp em bài này với ạ ![]() em cảm ơn !
em cảm ơn !
Khúc đầu bt lm vầy thoi còn đoạn sau sợ làm quá nó lố lăng nên để bn lm:3
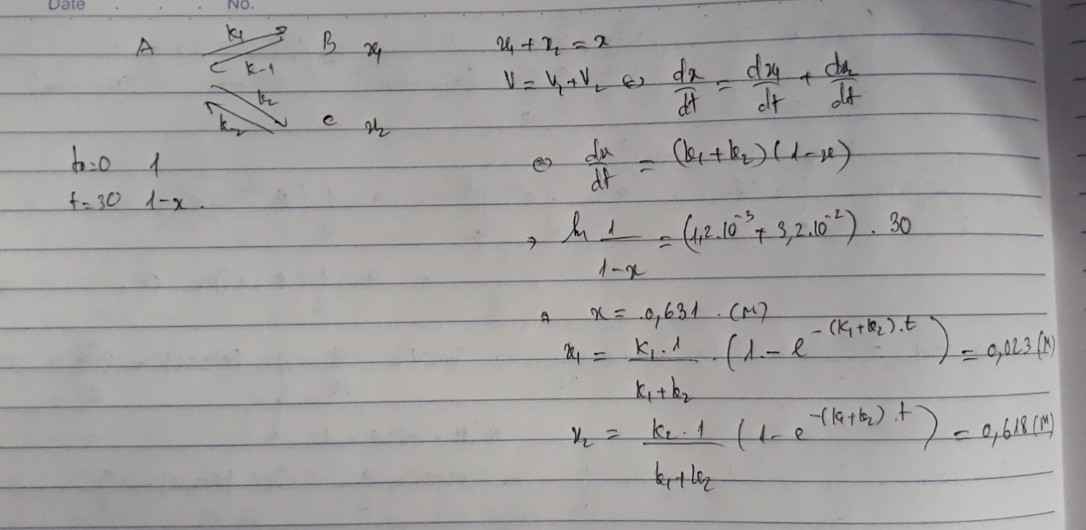
Đúng 2
Bình luận (7)






