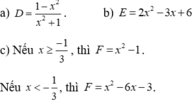Rút gọn biểu thức: C = |-3x| + 7x – 4 khi x ≤ 0
PB
Những câu hỏi liên quan
Rút gọn các biểu thức sau:a)
D
x
3
+
x
x
2
+
1
x
khi
x
0
;
b)
E...
Đọc tiếp
Rút gọn các biểu thức sau:
a) D = x 3 + x x 2 + 1 x khi x < 0 ;
b) E = 2 x 2 + 1 − − 3 x + 5 khi x ≥ 0 ;
c) F = x 2 − 3 x + 3 x + 1 − 2 .
Bài 1: Rút gọn biểu thức(3x + 1)(4x³ - 2x² + 1)(7x² + 3x)(2x + 4)
Đọc tiếp
Bài 1: Rút gọn biểu thức
(3x + 1)(4x³ - 2x² + 1)
(7x² + 3x)(2x + 4)
a: =12x^4-6x^3+3x+4x^3-2x^2+1
=12x^4-2x^3-2x^2+3x+1
b: =14x^4+28x^2+6x^2+12x
=14x^4+34x^2+12x
Đúng 0
Bình luận (0)
`@` `\text {Ans}`
`\downarrow`
\((3x + 1)(4x³ - 2x² + 1)\)
`= 3x(4x^3-2x^2+1) + 4x^3 - 2x^2 + 1`
`= 12x^4 - 6x^3 + 3x + 4x^3 - 2x^2 + 1`
`= 12x^4 + (-6x^3 + 4x^3) - 2x^2 + 3x + 1`
`= 12x^4 - 2x^3 - 2x^2 + 3x + 1`
\((7x² + 3x)(2x + 4)\)
`= 7x^2(2x+4) + 3x(2x+4)`
`= 14x^3 + 28x^2 + 6x^2 + 12x`
`= 14x^3 + (28x^2 + 6x^2)+12x`
`= 14x^3 + 34x^2 + 12x`
`@` `\text {Kaizuu lv uuu}`
Đúng 1
Bình luận (0)
Rút gọn biểu thức -9(x^2+7x-2)+(3x-1)(3x+1)
chọn biểu thức A=(x+5)(4-3x)-(3x+2)^2+(2x+1)^3-(2x-1)(4x^2+2x+1)
a)Rút gọn biểu thức A
b)Tính giá trị của A khi x=-3
c)tìm x để A=0
a: \(A=4x-3x^2+20-15x-9x^2-12x-4+\left(2x+1\right)^3-\left(8x^3-1\right)\)
\(=-12x^2-23x+16+8x^3+12x^2+6x+1-8x^3+1\)
\(=-17x+18\)
Đúng 0
Bình luận (0)
Cho bất phương trình - 4x + 12 0 . Phép biến đổi nào dưới đây đúng ?A. 4x 12B. x - 12C. 4x 12D. 4x - 12Khi x 0 , kết quả rút gọn của biểu thức |- 4x| - 3x + 13 là :A. x + 13B. 7x + 13C. - x + 13D. - 7x + 13
Đọc tiếp
Cho bất phương trình - 4x + 12 > 0 . Phép biến đổi nào dưới đây đúng ?
A. 4x < 12 | ||||
B. x < - 12 | ||||
C. 4x > 12 | ||||
D. 4x > - 12 Khi x < 0 , kết quả rút gọn của biểu thức |- 4x| - 3x + 13 là :
|
Cho bất phương trình - 4x + 12 > 0 . Phép biến đổi nào dưới đây đúng ?
- 4x + 12 < 0
<=> -4x < - 12
<=> 4x > 12
C
Khi x < 0 , kết quả rút gọn của biểu thức |- 4x| - 3x + 13 là : |
\(\left|-4x\right|-3x+13=-4x-3x+13=-7x+13\)
=> D
Đúng 2
Bình luận (0)
rút gọn biểu thức B=x^2-x/x^2-3x-7x-9/x^2-9
\(B=\dfrac{x^2-x}{x^2-3x}-\dfrac{7x-9}{x^2-9}\)
\(B=\dfrac{x\left(x-1\right)}{x\left(x-3\right)}-\dfrac{7x-9}{x^2-3^2}\)
\(B=\dfrac{x-1}{x-3}-\dfrac{7x-9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{7x-9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{\left(x-1\right)\left(x+3\right)-7x-9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x^2+3x-x-3-7x+9}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x^2-5x+6}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x\left(x-5\right)+6}{\left(x+3\right)\left(x-3\right)}\)
Đúng 0
Bình luận (1)
rút gọn biểu thức:
7x(x+4)-(7x+3)(2x ²-x+4)
\(=7x^2+28x-14x^3+7x^2-28x-6x^2+3x-12\)
\(=-14x^3+8x^2+3x-12\)
Đúng 1
Bình luận (0)
\(7x\left(x+4\right)-\left(7x+3\right)\left(2x^2-x+4\right)\)
\(=7x^2+28x-14x^3+7x^2-28x-6x^2+3x-12\)
\(=14x^3+8x^2+3x-12\)
Đúng 1
Bình luận (0)
Cho biểu thức C = (\(\dfrac{x}{x^2-x-6}\)-\(\dfrac{x-1}{3x^2-4x-15}\)) : \(\dfrac{x^4-2x^2+1}{3x^2+11x+10}\).(\(x^2\)-\(2x\)+1)
a) Rút gọn C
b)Tìm GTBT C với x = 2003
c) CMR C>0 khi x>3
a) \(C=\left(\dfrac{x}{x^2-x-6}-\dfrac{x-1}{3x^2-4x-15}\right):\dfrac{x^4-2x^2+1}{3x^2+11x+10}\cdot\left(x^2-2x+1\right)\) (ĐK: \(x\ne-\dfrac{5}{3};x\ne3;x\ne-2;x\ne1\))
\(C=\left[\dfrac{x}{\left(x-3\right)\left(x+2\right)}-\dfrac{x-1}{\left(x-3\right)\left(3x+5\right)}\right]:\dfrac{\left(x^2-1\right)^2}{\left(3x+5\right)\left(x+2\right)}\cdot\left(x-1\right)^2\)
\(C=\left[\dfrac{x\left(3x+5\right)}{\left(3x+5\right)\left(x+2\right)\left(x-3\right)}-\dfrac{\left(x-1\right)\left(x+2\right)}{\left(x-3\right)\left(3x+5\right)\left(x+2\right)}\right]\cdot\dfrac{\left(3x+5\right)\left(x+2\right)}{\left(x^2-1\right)^2\left(x-1\right)^2}\)
\(C=\dfrac{3x^2+5x-x^2-2x+x+2}{\left(3x+5\right)\left(x+2\right)\left(x-3\right)}\cdot\dfrac{\left(3x+5\right)\left(x+2\right)}{\left(x^2-1\right)^2\left(x-1\right)^2}\)
\(C=\dfrac{2x^2+4x+2}{\left(3x+5\right)\left(x+2\right)\left(x-3\right)}\cdot\dfrac{\left(3x+5\right)\left(x+2\right)}{\left(x+1\right)^2\left(x-1\right)^4}\)
\(C=\dfrac{2\left(x+1\right)^2}{\left(3x+5\right)\left(x-3\right)\left(x+2\right)}\cdot\dfrac{\left(3x+5\right)\left(x+2\right)}{\left(x+1\right)^2\left(x-1\right)^4}\)
\(C=\dfrac{2}{\left(x-1\right)^4\left(x-3\right)}\)
b) Thay x = 2003 ta có:
\(C=\dfrac{2}{\left(2003-1\right)^4\left(2003-3\right)}=\dfrac{2}{2002^4\cdot2000}=\dfrac{1}{2002^4\cdot1000}\)
c) \(C>0\) khi:
\(\dfrac{2}{\left(x-1\right)^4\left(x-3\right)}>0\) mà: \(\left\{{}\begin{matrix}2>0\\\left(x-1\right)^4>0\end{matrix}\right.\)
\(\Leftrightarrow x-3>0\)
\(\Leftrightarrow x>3\) (đpcm)
Đúng 2
Bình luận (0)
Cho biểu thức A =x2+4x+4/3x+6
a) Tìm điều kiện xác định của A b) Rút gọn biểu thức A. c)Tính giá trị của biểu thức A khi x =1/4
a) ĐKXĐ: 3x + 6 khác 0
x khác -2
b) A = (x² + 4x + 4)/(3x + 6)
= (x + 2)²/[3(x + 2)]
= (x + 2)/3
c) Khi x = 1/4, ta có:
A = (1/4 + 2)/3
= (9/4)/3
= 3/4
Đúng 2
Bình luận (0)