Chứng minh rằng số đo của một hình n-giác đều là n - 2 . 180 0 n
PB
Những câu hỏi liên quan
Chứng minh rằng số đo góc của hình n - giác đều là \(\dfrac{\left(n-2\right).180^0}{n}\)
Chứng minh rằng số đo góc của n-giác đều là
\(\frac{\left(n-2\right).180^o}{n}\)
tai vi cu n giac tao thanh n-2 tam giac
Đúng 0
Bình luận (0)
Chứng minh rằng số đo góc của hình n-giác đều là ( n- 2). 1800
Đúng 0
Bình luận (0)
a) Chứng minh tổng số đo các góc trong của một hình
n - giác là (n - 2)180°.
b) Tính tổng số đo các góc của một đa giác 12 cạnh.
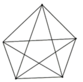
a)Vẽ các đường chéo xuất phát từ một đỉnh của n - giác, ta được (n - 2) tam giác.
Tổng các góc của hình n - giác bằng tổng các góc của (n - 2) tam giác, tức là có số đo bằng (n - 2).1800.
b) ta có: (n - 2).1800 = (12 - 2 ).1800 = 18000
Đúng 0
Bình luận (0)
Điền vào chỗ trống trong các câu sau :
a) Biết rằng tổng số đo các góc của một đa giác n cạnh là widehat{A}_1+widehat{A}_2+widehat{A}_3+.....+widehat{A}_nleft(n-2right).180^0. Vậy tổng số đo các góc của một đa giác 7 cạnh là .......
b) Đa giác đều là đa giác có .....
c) Biết rằng số đo mỗi góc của một đa giác đều n cạnh là dfrac{left(n-2right).180^0}{n}, vậy :
Số đo mỗi góc của ngũ giác đều là ..............
Số đo mỗi góc của lục giác đều là ..............
Đọc tiếp
Điền vào chỗ trống trong các câu sau :
a) Biết rằng tổng số đo các góc của một đa giác n cạnh là \(\widehat{A}_1+\widehat{A}_2+\widehat{A}_3+.....+\widehat{A}_n=\left(n-2\right).180^0\). Vậy tổng số đo các góc của một đa giác 7 cạnh là .......
b) Đa giác đều là đa giác có .....
c) Biết rằng số đo mỗi góc của một đa giác đều n cạnh là \(\dfrac{\left(n-2\right).180^0}{n}\), vậy :
Số đo mỗi góc của ngũ giác đều là ..............
Số đo mỗi góc của lục giác đều là ..............
a) Tổng số đo các góc của một đa giác n cạnh = \((7-2).180^0\) = \(900^0\)
b)Số đo mỗi góc của ngũ giác đều là : \(\frac{(5-2).180^0}{5}\)= \(108^0\)
Số đo mỗi góc của lục giác đều là \(\frac{(6-2).180^0}{6}\)= \(120^0\)
Đúng 0
Bình luận (0)
Giúp mình nha mình đang cần ghấp để làm đề cươngBài 9: Cho tam giác ABC vuông tại A, D là trung điểm của BC. Gọi M, N lần lượt là hình chiếu của điểm D trên cạnh AB, AC.a. Chứng minh tứ giác ANDM là hình chữ nhật.b. Gọi I, K lần lượt là điểm đối xứng của N, M qua D. Tứ giác MNKI là hình gì? Vì sao?c. Kẻ đường cao AH của tam giác ABC (H thuộc BC). Tính số đo góc MHN.Bài 10. Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.a. Chứng minh...
Đọc tiếp
Giúp mình nha mình đang cần ghấp để làm đề cương
Bài 9: Cho tam giác ABC vuông tại A, D là trung điểm của BC. Gọi M, N lần lượt là hình chiếu của điểm D trên cạnh AB, AC.
a. Chứng minh tứ giác ANDM là hình chữ nhật.
b. Gọi I, K lần lượt là điểm đối xứng của N, M qua D. Tứ giác MNKI là hình gì? Vì sao?
c. Kẻ đường cao AH của tam giác ABC (H thuộc BC). Tính số đo góc MHN.
Bài 10. Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.
a. Chứng minh rằng điểm E đối xứng với điểm M qua AB.
b. Các tứ giác AEMC, AEBM là hình gì? Vì sao?
c. Cho BC = 4cm, tính chu vi tứ giác AEBM
Bài 11. Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n – giác đều.
Bài 12. Tính số đo mỗi góc ngoài của lục giác đều.
Bài 13. Một hình chữ nhật có diện tích 15m2. Nếu tăng chiều dài 2 lần, tăng chiều rộng 3 lần thì diện tích sẽ thay đổi như thế nào?
Bài 14: Cho tam giác AOB vuông tại O với đường cao OM (M thuộc AB). CM: AB.OM = OA.OB.
Cho tam giác ABC có AB=AC và M là trung điểm của BC. Gọi N là trung điểm của AB trên tia đối của tia AC lấy điểm K sao cho NK=NC.
a) Chứng minh tam giác ABM=tam giác ACM
b) Chứng minh rằng AK=2.MC
c)Tính số đo của góc MAK
VẼ HÌNH LUÔN GIÚP MÌNH NHA!!!!!!!
THANK YOU
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Vẽ tam giác đều ABE, ADF nằm ngoài hình bình hành.
a/ Tính số đo góc ACF.
b/ Gọi O là giao điểm 2 đường chéo của hình bình hành ABCD. M, N lần lượt là trung điểm AE và AF. Chứng minh tam giác MON đều.
Giúp mình vớ!
Cho tam giác ABC có ba góc nhọn (AB < AC). Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi I là giao của CD và BE, K là giao của AB và DC.
1) Chứng minh rằng: DC = BE.
2) Gọi M và N lần lượt là trung điểm của CD và BE. Tính số đo góc BIK, góc AMN.
3) Chứng minh rằng IA là phân giác của góc DIE.
Bài 1: Lấy điểm M và N trên hai cạnh AB và BC của tam giác đều ABC sao cho MN//AC. Lấy điểm P trên cạnh AC sao cho góc CNP=60 độ. Chứng minh tứ giác AMNP là hình bình hành.
BÀi 2: Cho tam giác đều ABC. Lấy D thuộc AB, E thuộc AC, F thuộc BC sao cho góc EDF=60độ , và góc DFC=120 độ.
1) Tính số đo góc DEC
2) CHứng minh tứ giác DEFC là hình bình hành




