Thế nào là hàm đồng biến (nghịch biến) trên khoảng (a; b)?
PB
Những câu hỏi liên quan
Thế nào là hàm số đồng biến (nghịch biến) trên khoảng (a; b) ?
Hàm số đồng biến trên (a,b)
⇔ ∀x1, x2 ∈ (a, b): x1<x2 ⇒ f(x1) < f(x2)
Hàm số nghịch biến trên (a,b)
⇔ ∀x1, x2 ∈ (a, b): x1 < x2 ⇒ f(x1) > f(x2)
Đúng 0
Bình luận (0)
Cho hàm số:Khẳng định nào sau đây là đúng?A. Hàm số đồng biến trên từng khoảng xác định;B. Hàm số đồng biến trên khoảng (-
∞
;+
∞
);C. Hàm số nghịch biến trên từng khoảng xác định;D. Hàm số nghịch biến trên khoảng (-
∞
;+
∞
).
Đọc tiếp
Cho hàm số:
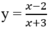
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
Cho hàm số:
y
x
-
2
x
+
3
Khẳng định nào sau đây là đúng?A. Hàm số đồng biến trên từng khoảng xác định;B. Hàm số đồng biến trên khoảng (-
∞
;+
∞
);C. Hàm số nghịch biến trên từng khoảng xác định;D. Hàm số nghịch biến trên...
Đọc tiếp
Cho hàm số: y = x - 2 x + 3
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
Cho hàm số . Khẳng định nào sau đây là khẳng định sai?A. Hàm số nghịch biến trên khoảng (-∞;-1)B. Hàm số nghịch biến trên khoảng (-1;dfrac{1}{2})C. Hàm số đồng biến trên mỗi khoảng (-∞;-1) và (dfrac{1}{2};+∞)D. Hàm số nghịch biến trên khoảng (-1;dfrac{1}{2})và đồng biến trên khoảng(dfrac{1}{2};+∞)
Đọc tiếp
Cho hàm số . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-∞;-1)
B. Hàm số nghịch biến trên khoảng (-1;\(\dfrac{1}{2}\))
C. Hàm số đồng biến trên mỗi khoảng (-∞;-1) và (\(\dfrac{1}{2}\);+∞)
D. Hàm số nghịch biến trên khoảng (-1;\(\dfrac{1}{2}\))và đồng biến trên khoảng(\(\dfrac{1}{2}\);+∞)
Bạn ghi lại hàm số đi bạn
Đúng 0
Bình luận (2)
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)
Đúng 3
Bình luận (0)
Cho hàm số y = x3 + 3x2 – 9x – 7 . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-3;1) .
B. Hàm số đồng biến trên (-9;-5).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên (5;+∞).
Tập xác định: D = R.
Ta có: 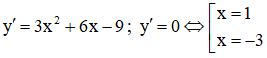
Bảng biến thiên:
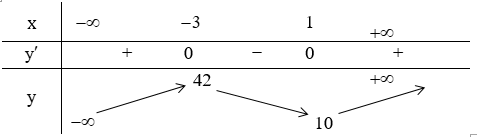
Kết luận: Hàm số đồng biến trên các khoảng: (-∞;-3),(1;+∞) . Hàm số nghịch biến trên khoảng (-3;1)
Chọn C.
Đúng 1
Bình luận (0)
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Đúng 0
Bình luận (0)
Khoảng nghịch biến của hàm số y= 1/2x^4-3x^2-3 là gì các bạn?
Hàm số y= x^2/1-x đồng biến trên khoảng nào?
Hàm số y= x^3+3x^2 nghịch biến trên khoảng nào?
Cho hàm số y = \(\sqrt{2x^2+1}\) Khẳng định nào đúngA: HS đồng biến trên khoảng (0;\(+\infty\))B: HS đồng biến trên khoảng (-\(\infty\);0)C: HS nghịch biến trên khoảng(0;+\(\infty\))D: HS nghịch biến trên khoảng(-1;1)
Xem chi tiết
Lời giải:
$y'=\frac{2x}{\sqrt{2x^2+1}}$
$y'>0\Leftrightarrow 2x>0\Leftrightarrow x>0$ hay $x\in (0;+\infty)$
$y'< 0\Leftrightarrow 2x< 0\Leftrightarrow x\in (-\infty;0)$
Vậy hàm số đồng biến trên $(0;+\infty)$ và nghịch biến trên $(-\infty; 0)$
Đáp án A.
Đúng 1
Bình luận (1)






