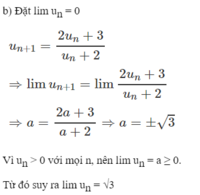Tìm giới hạn của dãy số ( u n ) với u n = 2 n - n 3 n + 1
PB
Những câu hỏi liên quan
Cho dãy số thực (un) xác định bởi \(\left\{{}\begin{matrix}u_1=2019\\u^2_n+2018u_n-2020u_{n+1}+1=0\left(n\in N\cdot\right)\end{matrix}\right.\). Tìm giới hạn của dãy số (Sn), biết: Sn = \(\dfrac{1}{u_1+2019}+\dfrac{1}{u_2+2019}+...+\dfrac{1}{u_n+2019}\)
Đề không cho sẵn dãy tăng à? Vậy phải chứng minh nó tăng trước
\(u_{n+1}=\dfrac{u_n^2+2018u_n+1}{2020}\)
\(u_{n+1}-u_n=\dfrac{u_n^2+2018u_n+1}{2020}-u_n=\dfrac{\left(u_n-1\right)^2}{2020}\ge0\) \(\Rightarrow\) dãy tăng và không bị chặn trên \(\Rightarrow lim\left(u_n\right)=+\infty\)
\(\Rightarrow2020u_{n+1}=u_n^2+2018u_n+1\)
\(\Leftrightarrow2020u_{n+1}-2020=u_n^2+2018u_n-2019\)
\(\Leftrightarrow2020\left(u_{n+1}-1\right)=\left(u_n+2019\right)\left(u_n-1\right)\)
\(\Rightarrow\dfrac{1}{2020\left(u_{n+1}-1\right)}=\dfrac{1}{\left(u_n+2019\right)\left(u_n-1\right)}=\dfrac{1}{2020}\left(\dfrac{1}{u_n-1}-\dfrac{1}{u_n+2019}\right)\)
\(\Rightarrow\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Thế n=1;2;...;n ta được:
\(\dfrac{1}{u_1+2019}=\dfrac{1}{u_1-1}-\dfrac{1}{u_2-1}\)
\(\dfrac{1}{u_2+2019}=\dfrac{1}{u_2-1}-\dfrac{1}{u_3-1}\)
...
\(\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Cộng vế: \(S_n=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}=\dfrac{1}{2018}-\dfrac{1}{u_{n+1}-1}\)
\(\Rightarrow\lim\left(S_n\right)=\dfrac{1}{2018}-\dfrac{1}{\infty}=\dfrac{1}{2018}\)
Đúng 1
Bình luận (0)
Cho dãy số (Un) được xác định như sau: \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\). Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó
Cho dãy số (Un) được xác định như sau \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\) . Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó
Cho dãy số
(
u
n
)
xác định bởi
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy số ( u n ) xác định bởi u 1 = 1 u n + 1 = 2 u n + 3 u n + 2 v ớ i n ≥ 1
a) Chứng minh rằng u n > 0 với mọi n.
b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
Cho dãy số (un) được xác định như sau: u1= 2017; un-1= n2(un-1 - un) với mọi n ∈ N*, n ≥2. Tìm giới hạn dãy số (un)
Lời giải:
$\frac{u_{n-1}}{u_n}=\frac{n^2}{n^2-1}>0$ với mọi $n\geq 2$ nên $u_{n-1}, u_n$ luôn cùng dấu.
Mà $u_1=2017>0$ nên $u_n>0$ với mọi $n=1,2,...$
Mặt khác:
$n^2(u_{n-1}-u_n)=u_{n-1}>0\Rightarrow u_{n-1}>u_n$ nên dãy $(u_n)$ là dãy giảm.
Dãy giảm và bị chặn dưới nên $u_n$ hội tụ. Đặt $\lim u_n=a$.
Ta có: $a=n^2(a-a)\Rightarrow a=0$
Vậy $\lim u_n=0$
Đúng 0
Bình luận (0)
Cho dãy số
(
u
n
)
xácđịnh bởi công thức truy hồi
u
1
2
u
n
+...
Đọc tiếp
Cho dãy số ( u n ) xácđịnh bởi công thức truy hồi u 1 = 2 u n + 1 = u n + 1 2 v ớ i n ≥ 1
Chứng minh rằng có giới hạn hữu hạn khi Tìm giới hạn đó.
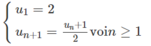
Ta có
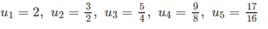
Dự đoán

Chứng minh dự đoán trên bằng quy nạp (bạn đọc tự chứng minh).
Từ đó
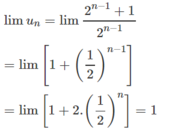
Đúng 0
Bình luận (0)
Cho dãy số
u
n
được xác định bởi
u
1
1
,
u
n
+
1
1
2
u
n
+
2
u
n...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 1 , u n + 1 = 1 2 u n + 2 u n với mọi n ≥ 1 . Tìm giới hạn của u n
A. l i m u n = 1
B. l i m u n = - 1
C. l i m u n = 2
D. l i m u n = - 2
Chọn C.
Phương pháp : Dãy số giảm bị chặn dưới thì có giới hạn.
Cách giải : Dễ thấy dãy số đã cho là dãy số dương.
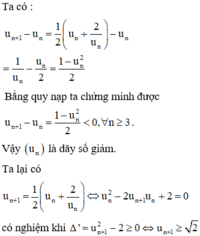
Vậy dãy số đã cho giảm và bị chặn dưới nên có giới hạn.
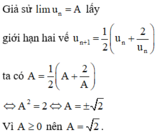
Đúng 0
Bình luận (0)
Câu 1:Dãy số (un) với undfrac{2^n-5.7^{n+1}}{2^n+7^n} có giới hạn bằng:A, 15 B, -25C, -35D, Một kết quả khácCâu 2:Dãy số (un) với undfrac{3^n-2.5^{n+1}}{2^n+7^n} có giới hạn bằng:A, -10B, -5C, 15D, Một kết quả khácCâu 3:Dãy số (un) với un sqrt[3]{dfrac{5-8n}{n+3}} có giới hạn bằng:A, -1B, -2C, 2D, -8
Đọc tiếp
Câu 1:
Dãy số (un) với un=\(\dfrac{2^n-5.7^{n+1}}{2^n+7^n}\) có giới hạn bằng:
A, 15
B, -25
C, -35
D, Một kết quả khác
Câu 2:
Dãy số (un) với un=\(\dfrac{3^n-2.5^{n+1}}{2^n+7^n}\) có giới hạn bằng:
A, -10
B, -5
C, 15
D, Một kết quả khác
Câu 3:
Dãy số (un) với un= \(\sqrt[3]{\dfrac{5-8n}{n+3}}\) có giới hạn bằng:
A, -1
B, -2
C, 2
D, -8
1/ \(\lim\limits\dfrac{\dfrac{2^n}{7^n}-5.7.\left(\dfrac{7}{7}\right)^n}{\dfrac{2^n}{7^n}+\left(\dfrac{7}{7}\right)^n}=-35\)
2/ \(\lim\limits\dfrac{\dfrac{3^n}{7^n}-2.5.\left(\dfrac{5}{7}\right)^n}{\dfrac{2^n}{7^n}+\dfrac{7^n}{7^n}}=0\)
3/ \(\lim\limits\sqrt[3]{\dfrac{\dfrac{5}{n}-\dfrac{8n}{n}}{\dfrac{n}{n}+\dfrac{3}{n}}}=\sqrt[3]{-8}=-2\)
Đúng 0
Bình luận (0)
Giới hạn của dãy số (
u
n
) với
u
n
3
n
3
+
2
n
-
1
2
n
2
-
n
, bằng A.
3
2
B. 0 C.
+
∞
D. 1
Đọc tiếp
Giới hạn của dãy số ( u n ) với u n = 3 n 3 + 2 n - 1 2 n 2 - n , bằng
A. 3 2
B. 0
C. + ∞
D. 1
Đáp án là C
Chia cả tử và mẫu cho n2 (n2 là lũy thừa bậc cao nhất của n trong mẫu thức), ta được :
u n = 3 n 3 + 2 n - 1 2 n 2 - n = 3 n + 2 n - 1 n 2 2 - 1 n
Do l i m 3 n + 2 n - 1 n 2 = + ∞ ; l i m 2 - 1 n = 2 > 0
Vậy l i m u n = + ∞
Cách 2: Ta có l i m u n = l i m n 3 3 + 2 n 2 - 1 n 3 n 2 2 - 1 n = l i m n 3 + 2 n 2 - 1 n 3 2 - 1 n
Vì l i m n = + ∞ và l i m 3 + 2 n 2 + 1 n 3 2 - 1 n = 3 2 > 0 nên theo quy tắc 2, l i m u n = + ∞
Đúng 0
Bình luận (0)
Giới hạn của dãy số
u
n
với
u
n
3
n
3
+
2
n
-
1
2
n
2
-
n
bằng A.
3
2
B. 0 C.
+
∞
D. 1
Đọc tiếp
Giới hạn của dãy số u n với u n = 3 n 3 + 2 n - 1 2 n 2 - n bằng
A. 3 2
B. 0
C. + ∞
D. 1
- Chia cả tử và mẫu cho n 2 ( n 2 là lũy thừa bậc cao nhất của n trong mẫu thức), ta được:
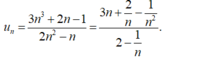
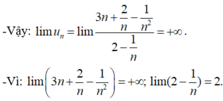
Chọn C
Đúng 0
Bình luận (0)