Tam giác ABC có ∠ A = 70 o , ∠ B = 30 o . Các đường phân giác BD, CE cắt nhau tại I. Khi đó số đo góc (ACI) là:
A. 100 o
B. 80 o
C. 40 o
D. 60 o
: Tam giác ABC có các góc A, B , C lần lượt tỉ lệ với các số 2; 3 và 4 thì số đo các góc của tam giác ABC là:
A. góc A bằng 40\(^o\); góc B bằng 60\(^o\) ; góc C bằng 80\(^o\)
B. góc A bằng 30\(^o\) ; góc B bằng 70\(^o\); góc C bằng 80\(^o\)
C. góc A bằng 80\(^o\); góc B bằng 60\(^o\); góc C bằng 40\(^o\)
A. góc A bằng 40*; góc B bằng 60*; góc C bằng 80*
tam giác ABC có góc A= 30\(^0\) , góc B = 70\(^o\). tính số đo góc C
tam giác ABC vuông góc tại A, có góc C = 40\(^o\). tính số đo gócB?
Bài 1:
Xét \(\Delta ABC\) có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(ĐL tổng 3 góc 1 \(\Delta\))
\(\Rightarrow30^o+70^o+\widehat{C}=180^o\) (Vì \(\widehat{A}=30^o;\widehat{B}=70^o\) (gt))
\(\Rightarrow\widehat{C}=180^o-30^o-70^o=80^o\)
Bài 2:
Xét \(\Delta ABC\) (vuông tại A) có:
\(\widehat{B}+\widehat{C}=90^o\) (Tc \(\Delta\) vuông)
\(\Rightarrow\widehat{B}+40^o=90^o\) (Vì \(\widehat{C}=40^o\) (gt))
\(\Rightarrow\widehat{B}=90^o-40^o=50^o\)
Giải:
+) Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) ( 3 góc của tam giác )
\(\Rightarrow30^o+70^o+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}=80^o\)
Vậy...
+) Ta có: \(\widehat{B}+\widehat{C}=90^o\) ( do tam giác có \(\widehat{A}=90^o\) )
\(\Rightarrow40^o+\widehat{B}=90^o\)
\(\Rightarrow\widehat{B}=50^o\)
Vậy...
Cho tam giác ABC có góc B=70o;gócC=30o.Tia phân giác của góc A cắt BC tại D.KẺ AH vuông góc BC(H thuộc BC).Tính góc BAC? góc HAD? góc ADH ?
Cho tam giác ABC có \(a = 10,\widehat A = {45^o},\widehat B = {70^o}\). Tính R,b,c.
Áp dụng định lí sin trong tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
\( \Rightarrow R = \dfrac{a}{{2\sin A}};\;\;b = \dfrac{{a.\sin B}}{{\sin A}}\)
Mà \(a = 10,\widehat A = {45^o},\widehat B = {70^o}\)
\( \Rightarrow R = \dfrac{{10}}{{2\sin {{45}^o}}} = 5\sqrt 2 ;\;\;b = \dfrac{{a.\sin {{70}^o}}}{{\sin {{45}^o}}} \approx 13,29\)
Mặt khác: \(\widehat A = {45^o},\widehat B = {70^o} \Rightarrow \widehat C = {65^o}\)
Từ định lí sin ta suy ra: \(c = \dfrac{{a.\sin C}}{{\sin A}} = \dfrac{{10.\sin {{65}^o}}}{{\sin {{45}^o}}} \approx 12,82.\)
Vậy \(R = 5\sqrt 2 ;\;\;b \approx 13,29\); \(c \approx 12,82.\)
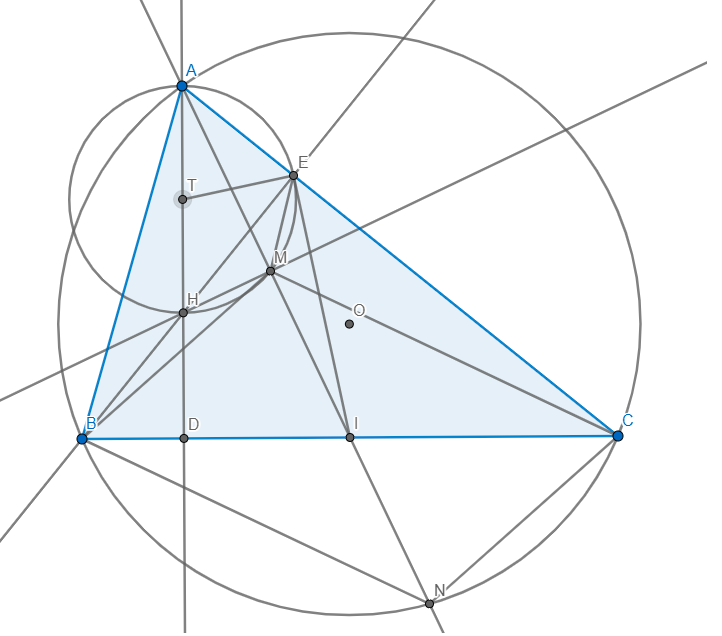
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Các đường cao AD và BE của tam giác ABC cắt nhau tại H. Gọi I là trung điểm của BC, vẽ HM vuông góc cới AI tại M.
a) Chửng minh tứ giác AHME nội tiếp và AE.AC = AM.AI;
b) Đường thẳng AI cắt đường tròn (O) tại điểm thứ hai là N. Chứng minh I là trung điểm của đoạn thẳng MN.
a) Ta có: \(\angle AMH=\angle AEH=90\Rightarrow AEMH\) nội tiếp
\(\Rightarrow\angle AME=\angle AHE\)
Ta có: \(\angle HEC+\angle HDC=90+90=180\Rightarrow HECD\) nội tiếp
\(\Rightarrow\angle AHE=\angle ACD\Rightarrow\angle AME=\angle ACD\Rightarrow MECI\) nội tiếp
\(\Rightarrow\angle AME=\angle ACI\)
Xét \(\Delta AME\) và \(\Delta ACI:\) Ta có: \(\left\{{}\begin{matrix}\angle AME=\angle ACI\\\angle CAIchung\end{matrix}\right.\)
\(\Rightarrow\Delta AME\sim\Delta ACI\left(g-g\right)\Rightarrow\dfrac{AM}{AC}=\dfrac{AE}{AI}\Rightarrow AE.AC=AM.AI\)
b) Gọi T là trung điểm AH
Dễ dàng chứng minh được T là tâm (AEMH)
\(\Rightarrow\Delta TEH\) cân tại T \(\Rightarrow\angle TEH=\angle THE=\angle ACB\) (HECD nội tiếp)
\(\Delta EBC\) vuông tại E có I là trung điểm BC cân tại I
\(\Rightarrow\Delta EBI\) cân tại I \(\Rightarrow\angle BEI=\angle EBI\)
mà \(\angle EBI+\angle ACB=90\Rightarrow\angle BEI+\angle TEH=90\Rightarrow\angle TEI=90\)
\(\Rightarrow IE\) là tiếp tuyến của (AEMH)
\(\Rightarrow\angle IAE=\angle IEM=\angle ICM\) (EMIC nội tiếp)
mà \(\angle IAE=\angle NBC\) (NBAC nội tiếp) \(\Rightarrow\angle ICM=\angle NBC\)
\(\Rightarrow CM\parallel BN\)
Tương tự \(\Rightarrow BM\parallel CN\) \(\Rightarrow BMCN\) là hình bình hành
mà I là trung điểm BC \(\Rightarrow I\) là trung điểm MN
Cho tam giác ABC, có góc A = 70o, góc C = 30o. Tia phân giác của góc B cắt Ac ở D.
a. Tính góc ABC và góc ADB.
b. Tia phân giác của góc C cắt AB ở E và cắt BD ở I. Tính góc BIC và góc CID.
Cho tam giác ABC vuông tại C có AB =5cm,ABC =60°, đường cao CK.Vẽ đường tròn tâm O đường kính CK , đường tròn (O ) cắt CB tại P (P khác C) a) Tính độ dài đoạn thẳng BC b) Chứng minh AB là tiếp tuyến của đường tròn (O) c)Tính khoảng cách từ O đến đường thẳng BC d) Từ B vẽ tiếp tuyến thứ hai BH với đường tròn (O) (H là tiếp điểm , H khác K ).Chứng minh tam giác BHP đồng dạng với tam giác BHC.
a: Xét ΔABC vuông tại C có
\(BC=AB\cdot\sin30^0=5\cdot\dfrac{1}{2}=2.5\left(cm\right)\)
a) Cho tam giác ABC vuông tại A. Tia phân giác BD chia AC thành 2 phần sao cho CD = 2AD. Tính số đo góc ABC.
b) Cho tam giác ABC có A = 70o, B = 60o. Đường tròn tâm O ngoại tiếp tam giác ABC. Tính số đo góc AOB.
a)
Theo tính chất đường phân giác áp dụng cho \(\Delta ABC\) có BD là phân giác góc ABC \(\Rightarrow\frac{AB}{BC}=\frac{AD}{DC}=\frac{1}{2}\)
\(\Delta ABC\) vuông tại A\(\Rightarrow\tan B=\frac{AB}{BC}=\frac{1}{2}\Rightarrow\widehat{B}\approx27\)
b,
Thấy \(\widehat{ACB}\) nội tiếp \(\left(O\right)\) chắn cung AB nhỏ
\(\Rightarrow\widehat{ACB}=\frac{1}{2}sđ\overline{AB}\left(1\right)\)
Thấy \(\widehat{AOB}\) chắn cung AB nhỏ \(\Rightarrow\widehat{AOB}=sđ\overline{AB}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{AOB}=2\widehat{ACB}=2\left(180^o-70^o-60^o\right)=2.50^o=100^o\)
Cho tam giác ABC có A=180o-3C,B=70o
a)Tính các góc của tam giác ABC
b)Vẽ tia phân giác của góc B cắt AC tại E.Qua E kẻ đường thẳng song song với BC cắt AB tại D.Cmr ED là tia phân giác của góc AEB.