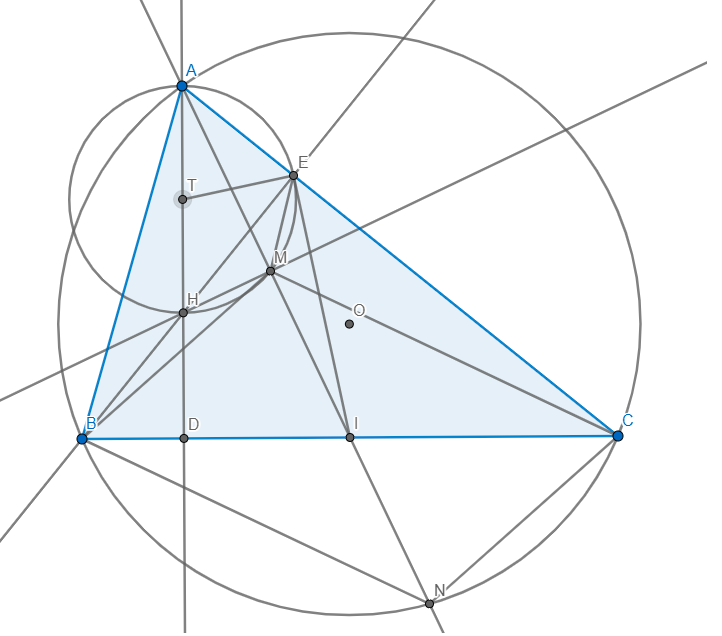
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Các đường cao AD và BE của tam giác ABC cắt nhau tại H. Gọi I là trung điểm của BC, vẽ HM vuông góc cới AI tại M.
a) Chửng minh tứ giác AHME nội tiếp và AE.AC = AM.AI;
b) Đường thẳng AI cắt đường tròn (O) tại điểm thứ hai là N. Chứng minh I là trung điểm của đoạn thẳng MN.
a) Ta có: \(\angle AMH=\angle AEH=90\Rightarrow AEMH\) nội tiếp
\(\Rightarrow\angle AME=\angle AHE\)
Ta có: \(\angle HEC+\angle HDC=90+90=180\Rightarrow HECD\) nội tiếp
\(\Rightarrow\angle AHE=\angle ACD\Rightarrow\angle AME=\angle ACD\Rightarrow MECI\) nội tiếp
\(\Rightarrow\angle AME=\angle ACI\)
Xét \(\Delta AME\) và \(\Delta ACI:\) Ta có: \(\left\{{}\begin{matrix}\angle AME=\angle ACI\\\angle CAIchung\end{matrix}\right.\)
\(\Rightarrow\Delta AME\sim\Delta ACI\left(g-g\right)\Rightarrow\dfrac{AM}{AC}=\dfrac{AE}{AI}\Rightarrow AE.AC=AM.AI\)
b) Gọi T là trung điểm AH
Dễ dàng chứng minh được T là tâm (AEMH)
\(\Rightarrow\Delta TEH\) cân tại T \(\Rightarrow\angle TEH=\angle THE=\angle ACB\) (HECD nội tiếp)
\(\Delta EBC\) vuông tại E có I là trung điểm BC cân tại I
\(\Rightarrow\Delta EBI\) cân tại I \(\Rightarrow\angle BEI=\angle EBI\)
mà \(\angle EBI+\angle ACB=90\Rightarrow\angle BEI+\angle TEH=90\Rightarrow\angle TEI=90\)
\(\Rightarrow IE\) là tiếp tuyến của (AEMH)
\(\Rightarrow\angle IAE=\angle IEM=\angle ICM\) (EMIC nội tiếp)
mà \(\angle IAE=\angle NBC\) (NBAC nội tiếp) \(\Rightarrow\angle ICM=\angle NBC\)
\(\Rightarrow CM\parallel BN\)
Tương tự \(\Rightarrow BM\parallel CN\) \(\Rightarrow BMCN\) là hình bình hành
mà I là trung điểm BC \(\Rightarrow I\) là trung điểm MN