Cho hình chóp S.ABCD có S A ⊥ A B C D và đáy ABCD là hình vuông. Từ A kẻ A M ⊥ S B . Khẳng định nào sau đây đúng?
A. A M ⊥ S B D
B. A M ⊥ S B C
C. S B ⊥ M A C
D. A M ⊥ S A D
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
Cho hình chóp S.ABCD có đáy ABCD là hình vuông , SA vuông góc (ABCD) . Kẻ AH vuông góc SB, AK vuông góc SD.
a. CMR : SC vuông góc (AHK)
b. Thiết diện cắt bởi (AHK) giao với hình chóp là hình gì
c. Tính S thiết diện biết đáy bằng a , SA= a căn 2
Cho hình chóp S.ABCD có S A ⊥ A B C D và đáy là hình vuông. Từ A kẻ A M ⊥ S B . Khẳng định nào sau đây đúng ?
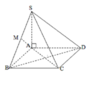
A. A M ⊥ S A D
B. A M ⊥ S B C
C. S B ⊥ M A C
D. A M ⊥ S B D
Đáp án là B.
A M ⊥ S B A M ⊥ B C do B C ⊥ S A B ⇒ A M ⊥ S B C .
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
a) Tính khoảng cách từ điểm \(S\) đến đường thẳng \(C{\rm{D}}\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\).
c) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\).
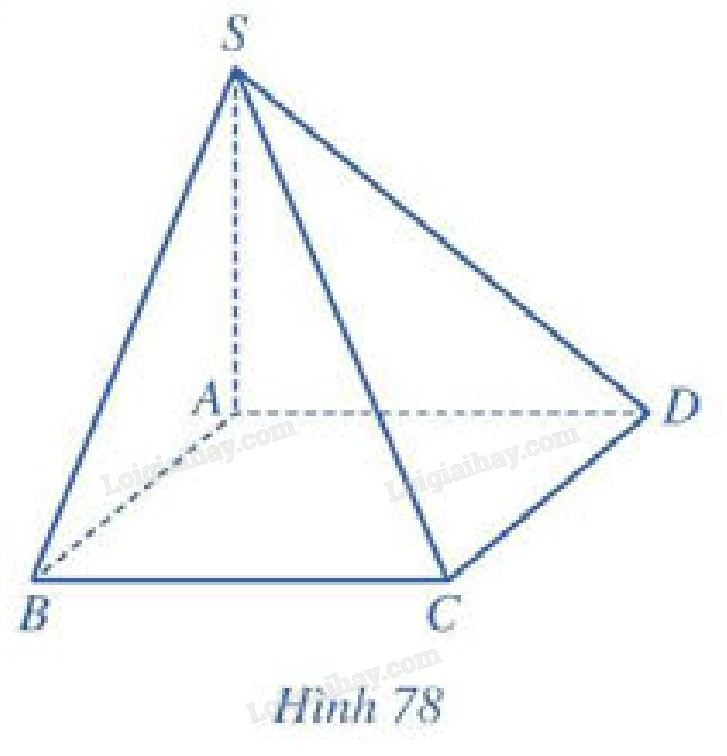
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, \(SD=\frac{3a}{2}\). Hình chiếu vuông góc của S lên mặt đáy (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp s.ABCD và khoảng cách từ A đến mặt phẳng (SBD)
Gọi H là trung điểm của AB, suy ra \(SH\perp\left(ACBD\right)\)
Do đó \(SH\perp HD\) ta có :
\(SH=\sqrt{SD^2-DH^2}=\sqrt{SD^2-\left(AH^2+AD^2\right)}=a\)
Suy ra \(V_{s.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{a^2}{3}\)
Gọi K là hình chiếu vuông góc của H trên BD và E là hình chiếu vuông góc của H lên SK. Ta có :
\(\begin{cases}BD\perp HK\\BD\perp SH\end{cases}\) \(\Rightarrow BH\perp\) (SHK)
=> \(BD\perp HE\) mà \(HE\perp SK\) \(\Rightarrow HE\perp\) (SBD)
Ta có : HK=HB.\(\sin\widehat{KBH}\)\(=\frac{a\sqrt{2}}{4}\)
Suy ra \(HE=\frac{HS.HK}{\sqrt{HS^2+HK^2}}=\frac{a}{3}\)
Do đó \(d\left(A:\left(SBD\right)\right)\)=2d(H; (SBD)) =3HE=\(\frac{2a}{3}\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA ⊥ ( A B C D ) và SA=2a.Tính khoảng cách d từ điểm B đến mặt phẳng (SCD).
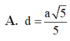
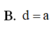
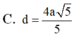
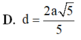
cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy SA=a căn 3 a)cm SAC vuông góc với SBD b)gọi AH là đg cao của tam giác SAB . cmr AK vuông góc với (SBC) c) tính góc giữa đg thẳng SC và mặt đáy ABC d) tính khoảng cách từ a đến mp (SCD)
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; S A ⊥ A B C D và SA=2a. Tính khoảng cách d từ điểm B đến mặt phẳng (SCD)
A. d = a 5 5 .
B. d = a
C. d = 4 a 5 5 .
D. d = 2 a 5 5 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; S A ⊥ A B C D và S A = 2 a . Tính khoảng cách d từ điểm B đến mặt phẳng (SCD).
A. d = a 5 5 .
B. d = a .
C. d = 4 a 5 5 .
D. d = 2 a 5 5 .
Đáp án D
Cách 1: Tư duy tự luận (Tính khoảng cách dựa vào hình chiếu)

Ta có
A B // C D A B ⊄ S C D C D ⊂ S C D ⇒ A B // S C D ⇒ d B , S C D = d A ; S C D
Lại có C D ⊥ A D , A D ⊂ S A D C D ⊥ S A , S A ⊂ S A D A D ∩ S A = A ⇒ C D ⊥ S A D .
Trong mặt phẳng (SAD) : Kẻ A H ⊥ S D , H ∈ S D thì C D ⊥ A H .
Suy ra A H ⊥ A C D ⇒ A H = d A ; S C D = d B ; S C D .
Δ S A D vuông tại A nên
1 A H 2 = 1 S A 2 + 1 A D 2 = 1 2 a 2 + 1 a 2 = 5 4 a 2 ⇒ A H = 2 a 5
Vậy khoảng cách từ điểm B đến mặt phẳng (SCD) là d = 2 a 5 5 .
Cách 2: Tư duy tự luận (Tinh khoảng cách qua công thức thể tích)
Thể tích khối chóp S.ABCD là V S . A B C D = 1 3 S A . S A B C D = 1 3 .2 a . a 2 = 2 a 3 3 (đvtt)
Do S Δ B C D = 1 2 S A B C D ⇒ V S . B C D = 1 2 V S . A B C D = a 3 3 (đvtt).
Ta có C D ⊥ S A D (xem lại phần chứng minh ở cách 1) ⇒ C D ⊥ S D ⇒ Δ S C D vuông tại D. Suy ra
S Δ S C D = 1 2 S D . C D = 1 2 S A 2 + A D 2 . C D = 1 2 . a . 2 a 2 + a 2 = a 2 5 2
(đvdt)
Mặt khác
V S . B C D = V B . S C D = 1 3 d B ; S C D . S Δ S C D ⇒ d B ; S C D = 3 V S . B C D S Δ S C D = 2 a 5
Vậy khoảng cách từ điểm B đến mặt phẳng (SCD) là d = 2 a 5 5 .