Tìm tham số m để đường thẳng d: y = 2x – 3m – 1 tiếp xúc với parabol (P): y = − x 2
A. m = 2 3
B. m = - 2 3
C. m = 3 2
D. m = - 3 2
Tìm giá trị thực của tham số m để đường thẳng d: y=2x+m tiếp xúc với parabol P: y=m−1x2+2mx+3m−1.
A.m=−1.
B.m=0.
C.m=2.
D.m=1.
Tìm giá trị thực của tham số m để đường thẳng d: y=2x+m tiếp xúc với parabol P: y=m−1x2+2mx+3m−1.
A.m=−1.
B m=0.
C.m=2.
D.m=1.
Xét ptr hoành độ của `(d)` và `(P)` có:
`(m-1)x^2+2mx+3m-1=2x+m`
`<=>(m-1)x^2+2(m-1)x+2m-1=0` `(1)`
`(d)` tiếp xúc `(P)<=>` Ptr `(1)` có nghiệm kép
`<=>{(a \ne 0),(\Delta'=0):}`
`<=>{(m-1 \ne 0),((m-1)^2-(m-1)(2m-1)=0):}`
`<=>{(m \ne 1),(-m(m-1)=0):}`
`<=>m=0`
`->B`
Phương trình hoành độ giao điểm : \(m-1x2+2mx+3m-1=2x+m\)
\(\Leftrightarrow m-1x2+2m-1x+2m-1=0\)
Để d tiếp xúc với P khi và chỉ khi phương trình có nghiệm kép
\(\Leftrightarrow m-1\ne0\Delta'=m-15-m-12m-1=-mm-1=0\) \(\Leftrightarrow m\ne1m=0m=1\Leftrightarrow m=0\)
\(\Rightarrow\) chọn \(B\)
Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x 2 và đường thẳng (d): y = 2x + m (m là tham số).
a) Xác định m để đường thẳng (d) tiếp xúc với parabol (P). Tìm hoành độ tiếp điểm.
parabol (P): y = x 2 ; đường thẳng (d): y = 2x + m (m là tham số).
a) phương trình hoành độ giao điểm của (P) và (d) là:
x 2 = 2x + m ⇔ x 2 - 2x - m = 0
Δ'= 1 + m
(d) tiếp xúc với (P) khi phương trình hoành độ giao điểm có duy nhất 1 nghiệm
⇔ Δ'= 1 + m = 0 ⇔ m = -1
Khi đó hoành độ giao điểm là x = 1
Tìm tham số m để đường thẳng d:y=2x - m tiếp xúc với parabol (P):y=x2
Phương trình hoành độ giao điểm (d) và (P):
\(x^2=2x-m\Leftrightarrow x^2-2x+m=0\) (1)
(d) tiếp xúc (P) khi và chỉ khi (1) có nghiệm kép
\(\Leftrightarrow\Delta'=1-m=0\)
\(\Rightarrow m=1\)
Tìm tham số m để đường thẳng d : y = 1 2 x + m tiếp xúc với parabol P : y = x 2 2
A. m = 1 4
B. m = - 1 4
C. m = 1 8
D. m = - 1 8
Tìm tham số m để đường thẳng d: y = 1 2 x + m tiếp xúc với parabol (P): y = x 2 2
A. m = 1 4
B. m = - 1 4
C. m = 1 8
D. m = - 1 8
1. Cho đường thẳng (d):y=2mx+2m-3 và Parabol (P):y=x\(^2\)
a) Tìm m để đường thẳng (d) đi qua A(1;5)
b) Tìm m để đường thẳng (d) tiếp xúc với Parabol (P)
a: Thay x=1 và y=5 vào (d), ta được:
2m+2m-3=5
=>4m-3=5
hay m=2
b: Phương trình hoành độ giao điểm là:
\(x^2-2mx-2m+3=0\)
Để(P) tiếp xúc với (d) thì \(\left(-2m\right)^2-4\left(-2m+3\right)=0\)
\(\Leftrightarrow4m^2+8m-12=0\)
\(\Leftrightarrow\left(m+3\right)\left(m-1\right)=0\)
=>m=-3 hoặc m=1
Cho parabol (P): y = x2 + x+ 2 và đường thẳng (d): y =ax + 1. Tìm tất cả các giá trị thực của tham số a để (P) tiếp xúc với (d).
A. a = -1; a = 3.
B. a = 2.
C. a = 1; a = -3.
D. Không tồn tại giá trị của a.
Xét phương trình hoành độ giao điểm: x2 + x+ 2 = ax + 1
x2 + (1 – a) x + 1 = 0
Để (P) tiếp xúc với (d) thì phương trình có nghiệm kép hay
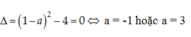
Chọn A.
cho đường thẳng (d): y=2mx+2m-3 và parabol (P): y=x^2 tìm m để đường thẳng tiếp xúc với parabol P
pt hoành độ giao điểm: \(x^2-2mx-2m+3=0\)
Để đường thẳng tiếp xúc với parabol thì pt có 1 nghiệm duy nhất
\(\Rightarrow\Delta'=0\)
\(\Delta'=m^2+2m-3=0\Rightarrow\left(m-1\right)\left(m+3\right)=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)