Xét phương trình hoành độ giao điểm: x2 + x+ 2 = ax + 1
x2 + (1 – a) x + 1 = 0
Để (P) tiếp xúc với (d) thì phương trình có nghiệm kép hay
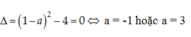
Chọn A.
Xét phương trình hoành độ giao điểm: x2 + x+ 2 = ax + 1
x2 + (1 – a) x + 1 = 0
Để (P) tiếp xúc với (d) thì phương trình có nghiệm kép hay
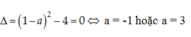
Chọn A.
Cho parabol (P): y = x 2 − 4x + 3 và đường thẳng d: y = mx + 3. Tìm tất cả các giá trị thực của mm để d cắt (P) tại hai điểm phân biệt A, B sao cho diện tích tam giác OAB bằng 9 2 .
A. m = 7.
B. m = −7.
C. m = −1,m = −7.
D. m = −1
Câu 1: Cho parabol (P):y=x^2+bx+c (b,c là các tham số thực)
a. Tìm giá trị của b,c biết parabol (P) đi qua điểm M(-3;2) và có trục đối xứng là đường thẳng x=-1
b. Với giá trị của b,c tìm được ở câu a), tìm m để đường thẳng d:y=-x-m cắt parabol(P) tại 2 điểm phân biệt A,B sao cho tam giác OAB vuông tại O( với O là gốc toạ độ)
Cho parabol (P): y = x 2 − 4x + 3 và đường thẳng d: y = mx + 3. Tìm giá trị thực của tham số m để d cắt (P) tại hai điểm phân biệt A, B có hoành độ x 1 , x 2 thỏa mãn x 1 3 + x 2 3 = 8
A. m = 2
B. m = -2
C. m = 4
D. Không có m
Gọi S là tập hợp tất các giá trị thực của tham số m để đường thẳng d : y = m x cắt parabol P : y = - x 2 + 2 x + 3 tại hai điểm phân biệt A và B sao cho trung điểm I của đoạn thẳng AB thuộc đường thẳng ∆ : y = x - 3 . Tính tổng tất cả các phần tử của S.
A. 2
B. 1
C. 5
D. 3
Tìm giá trị thực của tham số m để đường thẳng d: y=2x+m tiếp xúc với parabol P: y=m−1x2+2mx+3m−1.
A.m=−1.
B m=0.
C.m=2.
D.m=1.
Cho parabol \(\left(P\right):y=x^2+2x-3\)và đường thẳng \(\left(d\right):y=x+m\). Tìm tất cả giá trị m để (d) cắt (P) tại hai điểm phân biệt A, B nằm về hai phía của đường thẳng có phương trình y=1
Tìm giá trị thực của tham số m để đường thẳng d: y=2x+m tiếp xúc với parabol P: y=m−1x2+2mx+3m−1.
A.m=−1.
B.m=0.
C.m=2.
D.m=1.
Tìm tất cả các giá trị thực của tham số m để đường thẳng (d): y = (3m + 2)x -7m – 1 vuông góc với đường thẳng ( ∆ ) : y = 2 x - 1
A. m = 0.
B. ![]()
C. ![]()
D. 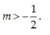
Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = (3m + 2)x − 7m − 1 vuông góc với đường △ : y = 2x − 1.
A. m = 0
B. m = - 5 6
C. m < 5 6
D. m > - 1 2