cho góc nhọn xOy. gọi M là 1 điểm thuộc tia phân giác của góc xOy. kẻ MA VUÔNG GÓC VỚI Ox; KẺ MB VUÔNG GÓC VỚI Oy
a, chứng minh MA = MB và tam giác OAB là tam giác cân
b, đường BM cắt Ox tại D , đường thẳng AM cắt Oy tại E . CHỨNG MINH MD=ME
NG
Những câu hỏi liên quan
Cho góc nhọn xOy. Gọi M là một điểm thuộc tia phân giác của góc xOy. Kẻ MA vuông góc với Ox ( A ϵ Ox), kẻ MB vuông góc với Oy ( B ϵ Oy). Tia AM cắt OB tại H, tia BM cắt OA tại K
a) Chứng minh : MA = MB
b) Chứng minh: △OAH = △OBK ; △OHK là tam giác gì? Vì sao?
c) Tính MK, biết OK = 10cm, OB =6 cm, MA = 3 cm .
d) Gọi G là trung điểm của HK. Chứng minh O, M, G thẳng hàng.
cho góc nhọn xOy. gọi M là 1 điểm thuộc tia phân giác của góc xOy. kẻ MA vuông góc Ox, kẻ MB vuông góc Oy
Chứng minh MA=MB và tam giác OAB cân
Đường thẳng BM cất Ox tại D, đường thẳng AM cắt Oy tại E. Chứng minh MD=ME
Chứng minh OM vuông góc DE
Câu b:Xét tam giác BME và tam giác AMD:
góc B = góc A
MB=MA
góc BME = góc AMD
suy ra: tam giác BME = tam giác AMD
suy ra: MD=ME
Câu a:Xét tam giác OBM và tam giác OAM ta có
OA chung
Góc BOM = góc AOM
góc B= góc A
suy ra: tam giác OBM = tam giác OAM
suy ra: MA=MB
và suy ra: OA=OB ; tam giác OAB là tam giác cân tại O vì OA=OB
Đúng 0
Bình luận (0)
Vẽ cái hình ra mún tính j thì tính
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho góc nhọn xoy gọi I là điểm thuộc tia phân giác của góc xoy kẻ ia vuông góc với ox kẻ ib vuông góc với oy gọi K là giao điểm của BI với OX gọi m là giao điểm của AI với OY chứng minh AB song song với MK
Bn viết rĩ hơn đc k
ngu\(\hept{\begin{cases}3\\3\end{cases}\hept{\begin{cases}5\\5\\5\end{cases}}5555555b5b5b55b}\)
Bài 4: (2 điểm) Cho góc nhọn xOy, kẻ tia phân giác Ot, lấy điểm M thuộc Ot. Kẻ MA vuông góc với Ox tại A, kẻ MB vuông góc với Oy tại B.. Chứng minh:
a) MA=MB và 
b) Gọi D là điểm đối xứng của M qua Ox, E là điểm đối xứng của M qua Oy. Cmr: OD=OE
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
góc AOM=góc BOM
=>ΔOAM=ΔOBM
=>MA=MB và OA=OB
b: M đối xứng D qua Ox
=>OM=OD
M đối xứng E qua Oy
=>OE=OM
=>OD=OE
Đúng 0
Bình luận (0)
Cho góc nhọn xOy và Ot là tia phân giác của góc xOy. Trên tia Ot lấy điểm M, kẻ MA vuông góc với Ox tại A, MB vuông góc với Oy tại B
a) Xét tam giác vuông AMO và tam giác vuông BMO :
góc MOA = góc MOB (gt)
OM là cạnh chung
=>tam giác vuông AMO = tam giác vuông BMO (cạnh huyền + góc nhọn)
=> OA=OB ( 2 cạnh tương ứng)
b) theo a) ta có : tam giác AMO = tam giác BMO
=>góc AMO = góc BMO
=> MO là tia phân giác của góc AMB
c) gọi C là giao điểm của OM và AB
Xét tam giác OAC và tam giác OBC có:
góc AOC = góc BOC (gt)
OC là cạnh chung
OA = OB (theo a)
=>tam giác OAC = tam giác OBC
=> góc ACO = góc BCO
mà hai góc này kề bù
=> góc ACO = góc BCO = 90 độ
=> OM vuông góc với AB
Đúng 2
Bình luận (3)
Cho góc nhọn xOy và Ot là tia phân giác của góc xOy. Trên tia Ot lấy điểm M, kẻ MA vuông góc với Ox tại A, MB vuông góc với Oy tại B
Câu 16: Cho góc nhọn xOy , gọi M là 1 điểm thuộc tia phân giác của góc xOy , kẻ MA vuông góc với Ox ( A thuộc Ox ) , MB vuông góc với (B thuộc Oy )
Chứng minh :
a , MA=MB : Tam giác OAB cân
b , BM cắt Ox tại D ; AM cắt Oy tại E . Chứng minh MD=ME
c, OM vuông góc với DE
tự kẻ hình nha
a) vì M thuộc tia phân giác của xOy=> M cách đều Ox,Oy=> MA=MB
xét tam giác OBM và tam giác OAM có
OBM=OAM(=90 độ)
OM chung
BOM=AOM( gt)
=> tam giác OBM= tam giác OAM(ch-gnh)
=> OA=OB( hai cạnh tương ứng)
=> tam giác ABO cân O
b) vì M thuộc tia phân giác của góc xOy=>ME=MD
c) vì BD,AE,OM cùng giao nhau tại M
mà BD,AE là đường cao => OM là đường cao ( 3 đường cao cùng đi qua một điểm)
=> OM vuông góc với DE
cho góc nhọn xoy . gọi M là một điểm thuộc tia phân giác của góc xoy . kẻ MA vuông góc với oy ( B ∈ oy)
a> chứng minh MA= MB và △ OAB cân
b> đường thảng BM cắt OX tại D , đường thẳng AM cắt OY tại E . chứng minh MD=ME
c> chứng minh OM vuông góc với DE
a: Xét ΔOMA vuông tại A và ΔOMB vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOMA=ΔOMB
Suy ra: MA=MB và OA=OB
hay ΔOBA cân tại O
b: Xét ΔOAE vuông tại A và ΔOBD vuông tại B có
OA=OB
\(\widehat{AOE}\) chung
Do đó: ΔOAE=ΔOBD
Suy ra: OD=OE
Xét ΔMAD vuông tại A và ΔMBE vuông tại B có
AD=BE
\(\widehat{MDA}=\widehat{MEB}\)
Do đó: ΔMAD=ΔMBE
Suy ra: MD=ME
c: Ta có: ΔODE cân tại O
mà OM là phân giác
nên OM vuông góc với DE
Đúng 1
Bình luận (1)
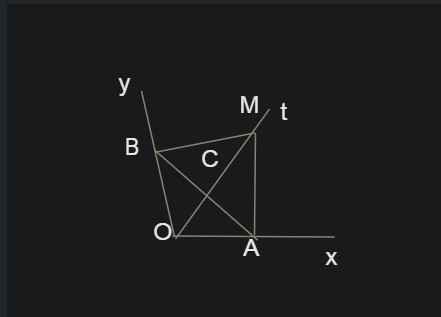
Bài 1: Cho góc nhọn xOy. Gọi C là một điểm thuộc tia phân giác của góc xOy, kẻ CA vuông
góc với Ox (A Ox), kẻ CB vuông góc với Oy (B Oy).
a) Chứng minh: CA = CB và tam giác OAB là tam giác cân.
b) Chứng minh OC vuông góc với AB
c) Gọi D là giao điểm của BC và Ox, E là giao điểm của AC và Oy. So sánh các độ dài CD
và CE.
d) Cho biết OC = 13cm, OA = 12cm. Tính độ dài AC.
a: Xét ΔOAC vuông tại A và ΔOBC vuông tại B có
OC chung
\(\widehat{AOC}=\widehat{BOC}\)
Do đó: ΔOAC=ΔOBC
Suy ra: OA=OB và CA=CB
=>ΔOAB cân tại O
b: Ta có: OA=OB
CA=CB
DO đó: OC là đường trung trực của AB
hay OC\(\perp\)AB
c: Xét ΔCAD vuông tại A và ΔCBE vuông tại B có
CA=CB
\(\widehat{ACD}=\widehat{BCE}\)
Do đó: ΔCAD=ΔCBE
SUy ra: CD=CE
Đúng 1
Bình luận (0)
Cho góc nhọn xOy. Gọi I là một điểm thuộc tia phân giác của góc xOy. Kẻ IA vuông góc với Ox (điểm A thuộc tia Ox) và IB vuông góc với Oy (điểm B thuộc tia Oy)a, Chứng minh IA IB. b, Cho biết OI 10cm, AI 6cm. Tính OA.c, Gọi K là giao điểm của BI và Ox và M là giao điểm của AI với Oy. So sánh AK và BM?d, Gọi C là giao điểm của OI và MK. Chứng minh OC vuông góc với MK.mình xin cả hình vẽ nhé
Đọc tiếp
Cho góc nhọn xOy. Gọi I là một điểm thuộc tia phân giác của góc xOy. Kẻ IA vuông góc với Ox (điểm A thuộc tia Ox) và IB vuông góc với Oy (điểm B thuộc tia Oy)
a, Chứng minh IA = IB. b, Cho biết OI = 10cm, AI = 6cm. Tính OA.
c, Gọi K là giao điểm của BI và Ox và M là giao điểm của AI với Oy. So sánh AK và BM?
d, Gọi C là giao điểm của OI và MK. Chứng minh OC vuông góc với MK.
mình xin cả hình vẽ nhé 