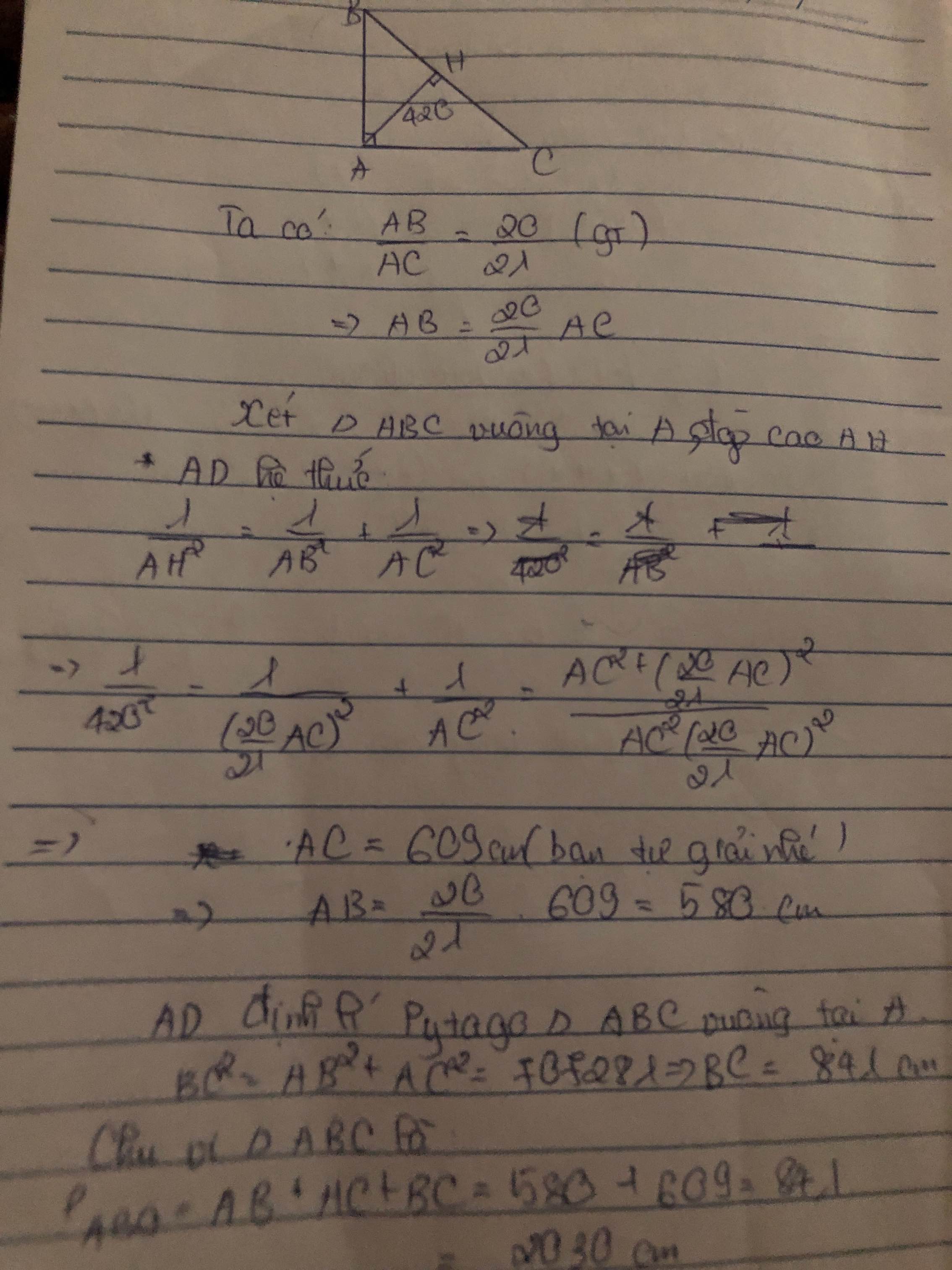2/AB/AC=3/4 nên AB=3AC/4(1)

Tam giác ABC vuông tại A, đường cao AH. Ta có: 1/AH2=1/AB2+1/AC2. Thay (1) vào rồi bạn giải phương trình sẽ tìm ra được AB, AC, BC từ đó sẽ ra chu vi tam giác ABC

Có:

\(\dfrac{AB}{AC}=\dfrac{4}{3}=\dfrac{4k}{3k}\) (k là số bất kì)

\(\Rightarrow AB=4k,AC=3k\)

Áp dụng đl pytago vào tam giác ABC được:

\(BC^2=AB^2+AC^2=\left(4k\right)^2+\left(3k\right)^2=16k^2+9k^2=25k^2=\left(5k\right)^2\\ \Rightarrow BC=5k\left(cm\right)\)

Theo hệ thức lượng, có:

\(AH.BC=AB.AC\\ \Leftrightarrow3,6.5k=4k.3k\\ \Leftrightarrow18=12k\\ \Rightarrow k=\dfrac{18}{12}=\dfrac{3}{2}\)

\(\Rightarrow\left\{{}\begin{matrix}AB=4k=4.\dfrac{3}{2}=6\left(cm\right)\\AC=3k=3.\dfrac{3}{2}=\dfrac{9}{2}=4,5\left(cm\right)\\BC=5k=5.\dfrac{3}{2}=\dfrac{15}{2}=7,5\left(cm\right)\end{matrix}\right.\)

\(\Rightarrow P_{ABC}=AB+AC+BC=6+4,5+7,5=18\left(cm\right)\)

Tam giác ABC vuông tại A, áp dụng hệ thức, ta có: 

    \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{18^2}=\frac{1}{324}\) (1)

Đặt \(\frac{AB}{AC}=\frac{3}{4}\Rightarrow\frac{AB}{3}=\frac{AC}{4}=k\Rightarrow AB=3k;AC=4k\)

Thế vào (1) ta được: \(\frac{1}{\left(3k\right)^2}+\frac{1}{\left(4k\right)^2}=\frac{1}{324}\)

                \(\Rightarrow\frac{9k^2+16k^2}{9k^2.16k^2}=\frac{1}{324}\)

               \(\Rightarrow\frac{15k^2}{144k^4}=\frac{1}{324}\Rightarrow\frac{15}{144k^2}=\frac{1}{324}\Rightarrow144k^2=4860\Rightarrow k^2=33,75\Rightarrow k=\frac{3\sqrt{15}}{2}\)

              \(\Rightarrow AB=\frac{3\sqrt{15}}{2}.3=\frac{9\sqrt{15}}{2}\) (cm)

                    AC = (3 √15)/2 . 4 = 6 √15 (cm)

Tam giác ABC vuông tại A, áp dụng định lý Pitago ta có:

       AB² + AC² = [(9 √15)/2]^2+(6 √15)^2= 3375/4 = BC²

=> BC = (15 √15)/2

Vậy chu vi của tam giác ABC là: AB+BC+AC= (9 √15)/2 + 6 √15 + (15 √15)/2 = 18 √15 (cm)

1: AB/AC=5/7

=>HB/HC=(AB/AC)^2=25/49

=>HB/25=HC/49=k

=>HB=25k; HC=49k

ΔABC vuông tại A có AH là đường cao

nên AH^2=HB*HC

=>1225k^2=15^2=225

=>k^2=9/49

=>k=3/7

=>HB=75/7cm; HC=21(cm)

\(\dfrac{AB}{AC}=\dfrac{20}{21}\Rightarrow AB=\dfrac{20AC}{21}\)

Áp dụng hệ thức lượng:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{841}{400AC^2}\)

\(\Rightarrow AC=609\) \(\Rightarrow AB=\dfrac{20}{21}AC=580\)

\(BC=\sqrt{AB^2+AC^2}=841\)

Chu vị: \(609+580+841=2030\)

Ta có: \(\dfrac{AB}{AC}=\dfrac{20}{21}\)

nên \(AB=\dfrac{20}{21}\cdot AC\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\dfrac{1}{\dfrac{400}{441}AC^2}+\dfrac{\dfrac{400}{441}}{\dfrac{400}{441}AC^2}=\dfrac{1}{176400}\)

\(\Leftrightarrow\dfrac{400}{441}AC^2=336400\)

\(\Leftrightarrow AC^2=370881\)

hay AC=609(cm)

\(\Leftrightarrow AB=\dfrac{20}{21}\cdot AC=\dfrac{20}{21}\cdot609=580\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=580^2+609^2=371461\)

hay BC=841(cm)

Chu vi tam giác ABC là:

AB+AC+BC=580+609+841=2030(cm)

1

\(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{.4}AC\)

Theo pytago xét tam giác ABC vuông tại A có:

\(\sqrt{AB^2+AC^2}=BC^2\\ \Rightarrow\sqrt{\left(\dfrac{3}{4}AC\right)^2+AC^2}=10\\ \Rightarrow AC=8\\ \Rightarrow AB=\dfrac{3.8}{4}=6\)

Theo hệ thức lượng xét tam giác ABC vuông tại A, đường cao AH có:

\(AB^2=BH.BC\\ \Leftrightarrow BH=\dfrac{AH^2}{BC}=\dfrac{6^2}{10}=3,6\)

2

\(\dfrac{AB}{AC}=\dfrac{27}{4}\Rightarrow AB=\dfrac{27}{4}AC\)

\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{27}{4}AC\right)^2+AC^2}=\dfrac{\sqrt{745}AC}{4}\) ( Theo pytago trong tam giác ABC vuông tại A)

Theo hệ thức lượng trong tam giác ABC vuông tại A, đường cao AH có:

\(AH.BC=AB.AC\\ \Leftrightarrow33,6.\dfrac{\sqrt{745}}{4}AC=\dfrac{27}{4}AC.AC\\ \Rightarrow AC=\dfrac{56\sqrt{745}}{45}\)

\(\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{27}{4}.\dfrac{56\sqrt{745}}{45}=\dfrac{42\sqrt{745}}{5}\\BC=\dfrac{\sqrt{745}}{4}.\dfrac{56\sqrt{745}}{45}=\dfrac{2086}{9}\end{matrix}\right.\)

Vậy \(\left\{{}\begin{matrix}AC\approx33,97\\AB\approx229,28\\BC\approx231,78\end{matrix}\right.\)

3

`BC=HB+HC=36+64=100`

Theo hệ thức lượng có (trong tam giác ABC vuông tại A đường cao AH):

\(AH^2=HB.HC\\ \Rightarrow AH=\sqrt{36.64}=48\)

\(AB=\sqrt{HB.BC}=\sqrt{36.100}=60\\ AC=\sqrt{HC.BC}=\sqrt{64.100}=80\)

Xét tam giác ABC vuông tại A:

\(BC^2=AB^2+AC^2\left(Pytago\right)\)

\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{20^2+15^2}=25\left(cm\right)\)

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A:

\(AH.BC=AB.AC\)

\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{20.15}{25}=12\left(cm\right)\)

Ta có: \(P_{ABC}=AB+AC+BC=20+15+25=60\left(cm\right)\)

toán lớp mấy ?

Chu vi tam giác ABC :

AHB + AHC = ABC

Thay số, ta được : 18+24 = 42 (cm)