ChoΔ ABC , góc A = 90 độ , AH⊥BC . Biết BH=9 , HC= 16 . Tính sinC , cosC , tanB
VA
Những câu hỏi liên quan
ChoΔ ABC , góc A = 90 độ , AH⊥BC . Biết BH=9 , HC= 16 . Tính sinC , cosC , tanB
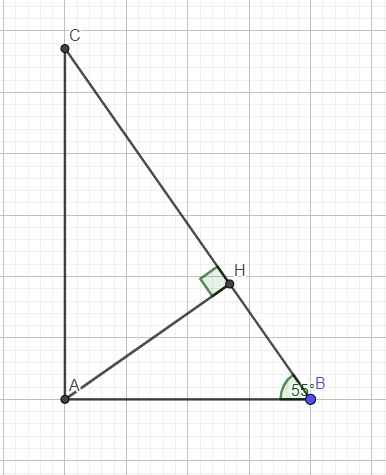
tam giác abc (góc a =90 độ) góc B=55 độ, bc=6 cm. kẻ AH vuông góc với bc. tính AH, BH, HC
Trong tam giác vuông ABC:
\(cosB=\dfrac{AB}{BC}\Rightarrow AB=BC.cosB\)
Trong tam giác vuông ABH:
\(sinB=\dfrac{AH}{AB}\Rightarrow AH=AB.sinB=BC.sinB.cosB=6.sin55^0.cos55^0\approx2,8\left(cm\right)\)
\(cosB=\dfrac{BH}{AB}\Rightarrow BH=AB.cosB=BC.\left(cosB\right)^2=6.\left(cos55^0\right)^2\approx1,2\left(cm\right)\)
\(CH=BC-BH=6-1,2=4,8\left(cm\right)\)
Đúng 2
Bình luận (0)
Tam giác ABC góc A=90 độ , AB =30cm , AC = 40cm
a) tính BC
b)kẻ AH vuông góc BC , tính AH , BH , HC
Xem chi tiết
góc A = 90 độ
suy ra tam giác ABC vuông tại A.
a) Áp dụng địng lý Pytago trong tam giác vuông ABC ta có: AB2 + AC2 = BC2
Mà AB = 40 cm, AC = 30 cm => BC = 50 cm
b)
Tính AH:
Diện tích tam giác ABC có thể được tính theo hai cách: \(\dfrac{1}{2}\)AB.AC hoặc \(\dfrac{1}{2}\)AH.BC
Suy ra: AH.BC = AB.AC
AH = 40.30:50 = 24 (cm).
Tính BH, CH:
Áp dụng định lý Pytago trong hai tam giác vuông AHB và AHC đều vuông tại H ta được:
+ AH2 + BH2 = AB2 => BH = \(\sqrt{\text{30^2 - 24^2}}\) = 18 (cm)
+ AH2 + CH2 = AC2 => CH = \(\sqrt{\text{40^2 - 24^2}}\) = 32
Đúng 3
Bình luận (0)
giải đề bài.cho tam giác abc(góc a=90 độ) đường cao ah,(h thuộc bc) biết ab=6cm,ah=4.8cm .tính bc=?;bh=?;ac=?;hc=?.
Theo định lí Pytago tam giác ABH vuông tại H ta có :
\(BH=\sqrt{AB^2-AH^2}=\sqrt{36-\left(4,8\right)^2}=\frac{18}{5}\)cm
Xét tam giác AHB và tam giác CHA ta có :
^AHB = ^CHA = 900
^BAH = ^HCA (cùng phụ ^HAC)
Vậy tam giác AHB ~ tam giác CHA ( g.g )
\(\frac{AH}{CH}=\frac{HB}{AH}\Rightarrow AH^2=HB.HC\)
\(\Rightarrow HC=\frac{AH^2}{HB}=\frac{\left(4,8\right)^2}{\frac{18}{5}}=\frac{32}{5}\)cm
=> \(BC=HC+HB=\frac{18}{5}+\frac{32}{5}=10\)cm
Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=\sqrt{100-36}=8\)cm
1.vẽ tam giác ABC vuông tại A, đg cao AH. Hãy tính BC,AH,AB,AC,cosB,cosC,sinB,sinC trong các trg hợp sau
1,CH=75cm ,góc C=30 độ 2, BH=2cm,góc B=45 độ
giải giúp mình với ajaaaa
mình đang cần gấp
Bài 1 Cho tam giác ABC vuông tại A có đường cao AH .biết BH = 9 cm ,HC = 16 cm .tính AH; AC ;số đo góc ABC (số đo góc làm tròn đến độ)
bài 2 Cho tam giác ABC vuông tại A , đường cao AH. biết AB = 3 cm ,AC = 4 cm. Tính độ dài các cạnh BC, AH và số đo góc ACB (làm tròn đến độ)
Bài 1:
AH=12cm
AC=20cm
\(\widehat{ABC}=37^0\)
Đúng 0
Bình luận (0)
tam giác ABC ,góc A = 90 độ . BH =1, CH= 3. tính AB, AC, AH, góc B
c/m: BH= CH. (cotB+tanB)
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9; HC = 16. Tính độ dài các đoạn thẳng AH, AB, AC, số đo góc B, góc C?
Cho tam giác ABC vuông tại A, AB= a (a>0 cho trước) góc ABC=60độa) Tính a theo độ dài các cạnh AC, BCb) Kẻ đường cao AH của tam giác ABC. Tính BH, HC theo ac)Tính sinC, suy ra độ dài đường cao AH
Xem chi tiết