Tìm x biết a. x4 – 16 = 0
b. x2 – 9x + 8 = 0
giúp mk vs
tìm x
a)x^4-2x^3-25x^2+50x=0
b)x^2(x-1)-4x^2+8x-4=0
c)9x^2-4-2(3x-2)^2=0
d)9x^2+90x+225-(x-7)^2=0
e)x^3-8+(x-2)(x+1)=0
g)(x+1)(x+2)(x+3)(x+4)-24=0
giúp mk vs ah
Tìm x biết
a,(x+4)(3x-5)=0
b, x2-2x+10x-20=0
c, 2x2+7x+3=0
GIÚP MÌNH VỚI NHA
Giai các bpt sau
a,(x+2)(x-3)>0
b,(x-1)(x+4)≤0
giúp mk vs ạ ai nhanh mk tick nka
a: (x+2)(x-3)>0
nên x+2;x-3 cùng dấu
=>x>3 hoặc x<-2
b: (x-1)(x+4)<=0
nên x-1 và x+4 khác dấu
=>-4<=x<=1
tìm x
a)x^2-x-12=0
b)x^2+3x-18=0
c)8x^2+30x+7=0
d)x^3-11x^2+30x=0
e)x^3-7x^2+15x-25=0
giúp mk vs ah!!!!!
a) Ta có: \(x^2-x-12=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
b) Ta có: \(x^2+3x-18=0\)
\(\Leftrightarrow\left(x+6\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-6\\x=3\end{matrix}\right.\)
Tìm x:
a) x2+9x=0
b) (x+4)2-16=0
c) x3-16x=0
d) x2-10x+25=0
\(a,\Leftrightarrow x\left(x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-9\end{matrix}\right.\\ b,\Leftrightarrow\left(x+4-4\right)\left(x+4+4\right)=0\\ \Leftrightarrow x\left(x+8\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\\ c,\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\\ d,\Leftrightarrow\left(x-5\right)^2=0\Leftrightarrow x=5\)
a) \(\Leftrightarrow x\left(x+9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-9\end{matrix}\right.\)
b) \(\Leftrightarrow x\left(x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)
c) \(\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
d) \(\Leftrightarrow\left(x-5\right)^2=0\\ \Leftrightarrow x=5\)
Tìm x:
a) 36x3-4x=0
b) 3x(x-2)-2+x=0
c) (x3-x2)-4x2+8x-4=0
d) x2-6x-16=0
e) x4-6x2-7=0
1) Tìm x, y, z
a) 9x2 +y2 + 2z2 – 18x +4z – 6y +20 = 0
b) 5x2 +5y2 +8xy+2y – 2x+2 = 0
c) 5x2 +2y2 + 4xy – 2x + 4y +5 = 0
d) x2 + 4y2 + z2 =2x + 12y – 4z – 14
e) x2 +y2 – 6x + 4y +2= 0
Giúp mik vs cần gấp!!!
\(a,\Leftrightarrow\left(9x^2-18x+9\right)+\left(y^2-6y+9\right)+\left(2z^2+4z+2\right)=0\\ \Leftrightarrow9\left(x-1\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\\z=-1\end{matrix}\right.\)
\(b,\Leftrightarrow\left(4x^2+8xy+4y^2\right)+\left(x^2-2x+1\right)+\left(y^2+2y+1\right)=0\\ \Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-y\\x=1\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(c,\Leftrightarrow\left(4x^2+4xy+y^2\right)+\left(x^2-2x+1\right)+\left(y^2+4y+4\right)=0\\ \Leftrightarrow\left(2x+y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x=-y\\x=1\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
a,9x^2+y^2+2z^2−18x+4z−6y+20=0
⇔9(x−1)^2+(y−3)^2+2(z+1)^2=0
⇔x=1;y=3;z=−1
b,5x^2+5y^2+8xy+2y−2x+2=0
⇔4(x+y)2+(x−1)2+(y+1)2=0
⇔x=−y;x=1y=−1⇔x=1y=−1
c,5x^2+2y^2+4xy−2x+4y+5=0
⇔(2x+y)^2+(x−1)^2+(y+2)^2=0
⇔2x=−y;x=1;y=−2
⇔x=1;y=−2
⇔(x−1)^2+(2y−3)^2+(z+2)^2=0
\(d,\Leftrightarrow\left(x^2-2x+1\right)+\left(4y^2-12y+9\right)+\left(z^2+4z+4\right)=0\\ \Leftrightarrow\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3}{2}\\z=-2\end{matrix}\right.\)
\(e,x^2+y^2-6x+4y+2=0\\ \Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
\(\Rightarrow\)PT vô nghiệm vì 11 không phải là tổng 2 số chính phương
Tìm x:
a) 36x3-4x=0
b) 3x(x-2)-2+x=0
c) (x3-x2)-4x2+8x-4=0
d) x2-6x-16=0
e) x4-6x2-7=0
(Mình cần gấp ạ)
a) Ta có: \(36x^3-4x=0\)
\(\Leftrightarrow4x\left(9x^2-1\right)=0\)
\(\Leftrightarrow x\left(3x-1\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=\dfrac{-1}{3}\end{matrix}\right.\)
b) Ta có: \(3x\left(x-2\right)+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-1}{3}\end{matrix}\right.\)
d) Ta có: \(x^2-6x-16=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
e) Ta có: \(x^4-6x^2-7=0\)
\(\Leftrightarrow\left(x^2-7\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow x\in\left\{\sqrt{7};-\sqrt{7}\right\}\)
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 3 x 2 − 8 x 3
b) y = 16x + 2 x 2 − 16 x 3 /3 − x 4
c) y = x 3 − 6 x 2 + 9x
d) y = x 4 + 8 x 2 + 5
a) TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔ 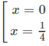
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )
b) TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 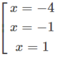
Bảng biến thiên:
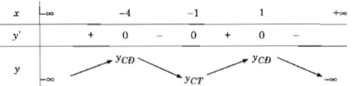
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
c) TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng ( - ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 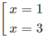
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)