y'= \(4x^3-4\left(m-1\right)x\)

Để hàm số đồng biến trên khoảng (1;3) thì \(y'\left(x\right)\ge0,\forall x\in\left(1;3\right)\)

\(\Leftrightarrow x^2-\left(m-1\right)\ge0,\forall x\in\left(1;3\right)\)

\(\Leftrightarrow m-1\le x^2,\forall x\in\left(1;3\right)\)

\(\Rightarrow m-1\le1\Leftrightarrow m\le2\)

Vậy \(m\in\) (−\(\infty\);2]

+) Điều kiện tanx ≠ m

Điều kiện cần để hàm số đồng biến trên (0; π/4) là m ∉ (0;1)

+) đạo hàm:

y ' = ( tan 2 x + 1 ) ( 2 - m ) ( tan x - m ) 2 = 2 - m cos 2 x . ( tan x - m ) 2

+) Ta thấy:

1 cos 2 x . ( tan x - m ) 2 > 0 ; ∀ m ∉ ( 0 ; 1 )   

+) Để hàm số đồng biến trên (0; π/4)

⇔ y ' > 0 m ∉ ( 0 ; 1 ) ⇔ - m + 2 > 0 m ≤ 0 ; m ≥ 1 ⇔ m ≤ 0   h o ặ c   1 ≤ m < 2

Chọn D.

1.

\(y'=m-3cos3x\)

Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)

\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)

\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)

\(\Leftrightarrow m\ge3\)

2.

\(y'=1-m.sinx\)

Hàm đồng biến trên R khi và chỉ khi:

\(1-m.sinx\ge0\) ; \(\forall x\)

\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)

- Với \(m=0\) thỏa mãn

- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)

\(\Rightarrow m\ge-1\)

- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)

\(\Rightarrow m\le1\)

Kết hợp lại ta được: \(-1\le m\le1\)

\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?

\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)

Hàm đồng biến trên các khoảng xác định khi và chỉ khi:

\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)

\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)

\(\Leftrightarrow m\le-\dfrac{1}{2}\)

Đáp án D

Điều kiện: x ≠ m .

Đạo hàm y ' = − m 2 + 4 x − m 2 ;

Hàm số đồng biến trên khoảng  1 ; + ∞ ⇔ y ' > 0, ∀ x ∈ 1 ; + ∞ x ≠ m

⇔ − m 2 + 4 > 0, ∀ x ∈ 1 ; + ∞ x ≠ m ⇔ − 2 < m < 2 m ∉ 1 ; + ∞ ⇔ m ∈ − 2 ; 1

Chọn D

.

Đặt với , , .

Vậy .

Chọn B.

Tập xác định D = R.

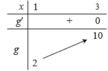
Dựa vào bảng biến thiên, kết luận: m ≤ min ⁡g(x) ⇔ m ≤ 2