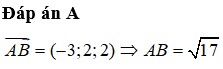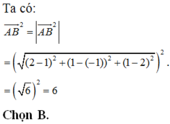1 trong ko gian oxyz, cho 2 điểm A(1;-2;-3) và B(3;0;1). Phương trình mặt cầu đường kính AB là
2 Trong ko gian oxyz, cho ba điểm A (1;2;1) B(3;1;0),C (3;-1;2) .Phương ttrinh chính tắc của đường thẳng vuông góc với mặt phẳng (ABC) tại A là
3 trong ko gian oxyz, vecto nào sau đây là véc tơ pháp tuyến của mp đi qua ba điểm A(2;-1;4) B(1;0;1),C(4;1;6)
A \(\overline{n}\left(1;1;2\right)\) \(\overline{n}\left(1;1;2\right)\) B \(\overline{N}\left(-2;1;1\right)\) C \(\overline{N}\left(1;1;-1\right)\) D \(\overline{N}\left(-1;1;1\right)\)
4 cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a.Thể tích của khối nón đã cho bằng bao nhiêu
5 cho hình nón tròn xoay có độ dài đường sinh là 2a, góc ở đỉnh của hình nón bằng \(60^0\) .tHỂ tích V của khối nón đã cho là
6 trong ko gian, cho tam giác vuông ABC vuông tại A , AB =a ,AC =\(a\sqrt{3}\) . Tính độ dài đường sinh l của hình nón, nhận dc khi qay tam giác ABC xung quanh trục AB
7 trong ko gian cho tam giác ABC vuông tại A, AB=a, \(\widehat{ACB}=30^0\) . Tính thể tích V của khối nón nhận dc khi quay quanh tam giác ABC quanh cạnh AC
8 Cho tứ diện đều ABCD có cạnh bằng 3a. Hình nón (N) có đỉnh A có đáy là đường tròn ngoại tiếp tam giác BCD .tính diện tích xung quanh Sxq của (N)
9 cho hình nón đỉnh S có đáy là hình tròn O, thiết diện qua trục là tam giác đều cạnh a. Thể tích của khối nón bằng
10 cắt mộ hình nón bằng một mặt phảng đi qua trục của nó ta dc thiết diện là một tam giác vuông can có cạnh huyền bằng a.Diện tích xung quanh hình nón theo a là