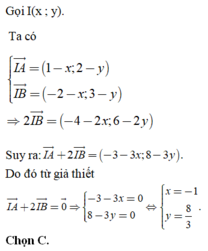trong hệ tọa độ oxy cho 3 điểm D(2;-1), E(2;2); F(-2;2) lần luọt là chân đường cao hạ từ các đỉnh A,B,C của tam giác ABC.Tìm Tổng hoành độ 3 đỉnh của tam giác ABC
CL
Những câu hỏi liên quan
trong hệ tọa độ oxy , cho 3 điểm a(1;1),b(3;2),c(6;5) . tìm tọa độ điểm D để tứ giác ABCD là hình bình hành
ABCD là hình bình hành
=>vecto AB=vecto DC
=>6-x=3-1=2 và 5-y=2-1=1
=>x=4 và y=4
Đúng 0
Bình luận (0)
Trong hệ tọa độ Oxy cho HBH ABCD, biết A(1;3); B(-2;0), C(2;-1). Tìm tọa độ điểm D
Trong hệ tọa độ Oxy, cho bốn điểm A(-5; -2), B(-5; 3), C(3; 3), D(3; -2) Khẳng định nào sau đây đúng? A.
A
B
→
,
C
D
→
cùng hướng. B. ABCD là hình chữ nhật. C. I(-1 ; 1) là trung điểm AC D.
O
A
→
+
O
B...
Đọc tiếp
Trong hệ tọa độ Oxy, cho bốn điểm A(-5; -2), B(-5; 3), C(3; 3), D(3; -2) Khẳng định nào sau đây đúng?
A. A B → , C D → cùng hướng.
B. ABCD là hình chữ nhật.
C. I(-1 ; 1) là trung điểm AC
D. O A → + O B → = O C → .

Dùng phương pháp loại trừ ta Chọn B.
Đáp án B
Đúng 0
Bình luận (0)
Trong hệ tọa độ Oxy, cho hai điểm A(2 ; -3) ; B ( 4 ; 7). Tìm tọa độ trung điểm I của đoạn thẳng AB
A. I( 6 ; 4)
B. I (2 ; 10)
C. I (3 ; 2)
D. I( 8; -21)
x I = 2 + 4 2 = 3 y I = − 3 + 7 2 = 2 ⇒ I 3 ; 2 .
Đáp án C
Đúng 0
Bình luận (0)
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3) ; B(4; 7). Tìm tọa độ trung điểm I của đoạn thẳng AB?
A. (6; 4)
B.(2; 10)
C. (3; 2)
D.( 8; -21)
x I = 2 + 4 2 = 3 y I = − 3 + 7 2 = 2 ⇒ I 3 ; 2 .
Đáp án C
Đúng 0
Bình luận (0)
Trong hệ tọa độ Oxy, cho hai điểm A(1; 2) ; B(- 2; 3). Tìm tọa độ đỉểm I sao cho
I
A
→
+
2
I
B
→
0
→
.
A.
I
1
;
2
.
B.
I
1
;...
Đọc tiếp
Trong hệ tọa độ Oxy, cho hai điểm A(1; 2) ; B(- 2; 3). Tìm tọa độ đỉểm I sao cho I A → + 2 I B → = 0 → .
A. I 1 ; 2 .
B. I 1 ; 2 5 .
C. I − 1 ; 8 3 .
D. I 2 ; − 2 .
Trong mặt phẳng Oxy cho parabol ( P ) : y = 1 4 x 2 và đường thẳng d : y = x + 3.
1) Vẽ (P) và d trên cùng một hệ trục tọa độ.
2) Tìm tọa độ giao điểm của (P) và d.
1) Xác định được ít nhất hai điểm phân biệt thuộc đường thẳng d. Chẳng hạn: A ( − 3 ; 0 ) ; B ( 0 ; 3 ) .
Xác định được đỉnh và ít nhất hai điểm thuộc (P) . Chẳng hạn : O ( 0 ; 0 ) ; C ( 6 ; 9 ) ; E ( − 6 ; 9 ) .
Đồ thị
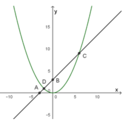
2) Phương trình hoành độ giao điểm: 1 4 x 2 = x + 3 ⇔ 1 4 x 2 − x − 3 = 0 ⇔ x = − 2 hoặc x= 6
Tọa độ giao điểm là D ( − 2 ; 1 ) v à C ( 6 ; 9 ) .
Đúng 0
Bình luận (0)
trong hệ tọa độ oxy cho 3 điểm a (1;3), B (4;0), C (2; -5). Tìm tọa độ điểm M thỏa mãn hệ thức vecto MA + vecto MB - 3 vecto MC = vecto 0 ?
trong hệ tọa độ oxy cho 3 điểm a (1;3), B (4;0), C (2; -5). Tìm tọa độ điểm M thỏa mãn hệ thức vecto MA + vecto MB - 3 vecto MC = vecto 0 ?
Gọi tọa độ điểm \(M\) là \(M\left(x;y\right).\)
\(\overrightarrow{MA}=\left(1-x;3-y\right);\overrightarrow{MB}=\left(4-x;-y\right);\overrightarrow{MC}=\left(2-x;-5-y\right).\)
Ta có: \(\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=\overrightarrow{0}.\)
\(\left\{{}\begin{matrix}1-x+4-x-3\left(2-x\right)=0.\\3-y-y-3\left(-5-y\right)=0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-2x+5-6+3x=0.\\3-2y+15+3y=0.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=0.\\y+18=0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1.\\y=-18.\end{matrix}\right.\) \(\Rightarrow M\left(1;-18\right).\)
Đúng 1
Bình luận (0)
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3); B (3; 4) Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng. A. M (1 ; 0) B. M(4; 0) C.
M
−
5
3
;
−
1
3
.
D.
M
17
7
;
0...
Đọc tiếp
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3); B (3; 4) Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng.
A. M (1 ; 0)
B. M(4; 0)
C. M − 5 3 ; − 1 3 .
D. M 17 7 ; 0 .