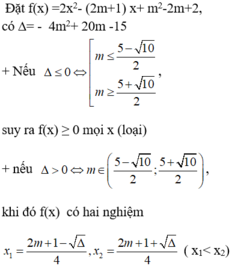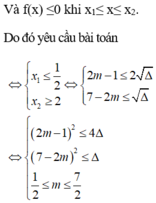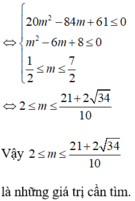Tìm giá trị m để bpt x2+(m+1)x+2m+7>0 có nghiệm với mọi x
HN
Những câu hỏi liên quan
Câu 1 : tìm m để BPT ( m - 1 )x2 + 2 ( m - 2 )x - 1 > 0 nghiệm đúng với mọi x ∈ R
Câu 2 : tìm m để BPT ( m - 1 )x2 + 2 ( m - 2 )x - 1 ≥ 0 vô nghiệm .
Giúp em với ạ . ThanksU <33
a, Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m-1>0\\\Delta'=m^2-4m+4+m-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left(m-\dfrac{3}{2}\right)^2< -\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn
b, Yêu cầu bài toán thỏa mãn khi phương trình \(\left(m-1\right)x^2+2\left(m-2\right)x-1< 0\) có nghiệm với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m-1< 0\\\Delta'=m^2-3m+3< 0\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn
Đúng 1
Bình luận (0)
tìm tất cả các giá trị của m để bpt sau nghiệm đúng với mọi giá trị của x
\(\frac{-3x^2+5x-4}{\left(m-4\right)x^2+\left(1+m\right)x+2m-1}>0\)
1/ Tìm các giá trị của tham số m để bpt ( m-1) x^2- ( m-1) x+1>0 nghiệm đúng vs mọi giá trị của x. 2/ Tìm giá trị của tham số m để pt x^2 - ( m-2) x+m^2 -4m=0 có 2 nghiệm trái dấu. 3/ Tìm giá trị của tham số m để pt x^2 -mx+1=0 có 2 nghiệm phân biệt.
Bài 2:
Để phương trình có hai nghiệm trái dấu thì (m-2)(m+2)<0
hay -2<m<2
Đúng 0
Bình luận (0)
1.Tìm m để bpt \(2\left|x-m\right|+x^2+2>2mx\) thỏa mãn với mọi x
2. Tìm m để bpt : \(x^2+2\left|x+m\right|+2mx+3m^2-3m+1< 0\) có nghiệm
1.
\(2\left|x-m\right|+x^2+2>2mx\)
\(\Leftrightarrow\left(x-m\right)^2+2\left|x-m\right|-m^2+2>0\)
\(\Leftrightarrow t^2+2t-m^2+2>0\left(t=\left|x-m\right|\ge0\right)\)
\(\Leftrightarrow m^2< f\left(t\right)=t^2+2t+2\)
Yêu cầu bài toán thỏa mãn khi \(m^2< minf\left(t\right)=2\)
\(\Leftrightarrow-\sqrt{2}< m< 2\)
Vậy \(-\sqrt{2}< m< 2\)
Đúng 0
Bình luận (0)
2.
\(x^2+2\left|x+m\right|+2mx+3m^2-3m+1< 0\)
\(\Leftrightarrow\left(x+m\right)^2+2\left|x+m\right|+2m^2-3m+1< 0\)
\(\Leftrightarrow\left(\left|x+m\right|+1\right)^2< -2m^2+3m\)
Ta có \(VT=\left(\left|x+m\right|+1\right)^2=\left(-\left|x+m\right|-1\right)^2\le\left(-1\right)^2=1\)
Yêu cầu bài toán thỏa mãn khi \(VP=-2m^2+3m>1\)
\(\Leftrightarrow2m^2-3m+1< 0\)
\(\Leftrightarrow\dfrac{1}{2}< m< 1\)
Đúng 0
Bình luận (0)
Cho phương trình x2+(2m-1)x-m=0 (1)
a)Chứng minh phương trình (1) luôn có nghiệm với mọi m
b)Gọi x1;x2 là hai nghiệm của phương trình (1).Tìm giá trị của m để biểu thức
A=x12+x22-x1x2 có giá trị nhỏ nhất
a: Δ=(2m-1)^2-4*(-m)
=4m^2-4m+1+4m=4m^2+1>0
=>Phương trình luôn có nghiệm
b: \(A=\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2\)
\(=\left(2m-1\right)^2-3\left(-m\right)\)
=4m^2-4m+1+3m
=4m^2-m+1
=4(m^2-1/4m+1/4)
=4(m^2-2*m*1/8+1/64+15/64)
=4(m-1/8)^2+15/16>=15/16
Dấu = xảy ra khi m=1/8
Đúng 1
Bình luận (0)
Tìm m để bpt 2x2- (2m+1) x+ m2-2m+2≤ 0 nghiệm đúng với mọi
x
∈
1
2
;
2
A.
2
≤
m
≤
21
+
2
34
10
B.
m
≤...
Đọc tiếp
Tìm m để bpt 2x2- (2m+1) x+ m2-2m+2≤ 0 nghiệm đúng với mọi x ∈ 1 2 ; 2
A. 2 ≤ m ≤ 21 + 2 34 10
B. m ≤ 21 + 2 34 10
C. m ≥ 2
D. 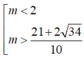
Cho phương trình : x² - 2( m-1)x - 2m=0(I) a. Chứng tỏ rằng phương trình (I) luôn có hai nghiệm phân biệt với mọi giá trị m b. Tính X1 + X2 ; X1.X, theo m c. Tìm m để x1² + x2² = 4
a: Δ=(2m-2)^2-4*(-2m)
=4m^2-8m+4+8m=4m^2+4>0
=>Phương trình luôn có hai nghiệm phân biệt
b: x1+x2=2m-2; x1x2=-2m
c: x1^2+x2^2=4
=>(x1+x2)^2-2x1x2=4
=>(2m-2)^2-2*(-2m)=4
=>4m^2-8m+4+4m=4
=>4m^2-4m=0
=>m=0 hoặc m=1
Đúng 0
Bình luận (0)
cho phương trình x^2 -(2m-1)x -m =0
giải phương trình với m=2
c/m pguwowng trình trên luôn có hai nghiệm phân biệt x1, x2 với mọi giá trị của m
tìm giá trị của m để A= x1^2 +x2^2 -6x1x2 đạt giá trị nhỏ nhất
thay m=2 vào ta được phương trình:
x2-3x-2=0 <bấm máy>
* CM: delta=b2-4ac=(2m-1)2-4.1.(-m)= 4m2-4m+1+4m=4m2+1
ta thấy m2 >=0 <=> 4m2>=0 <=> 4m2+1>=1>0 <=> delta>0 Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m.
* >=: lớn hơn hoặc bằng. <đề còn lại ghi k rõ nên mình k giúp được =))>
Đúng 0
Bình luận (0)
Cho phương trình x2 – 2(m – 1)x + 2m – 5 = 0 (m là tham số)
1/ Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m
2/ Tìm các giá trị của m để phương trình có hai nghiệm trái dậu
3/ Với giá trị nào của m thì biểu thức A = x12 + x22 đạt giá trị nhỏ nhất. Tìm giá trị đó
a/ Xét pt :
\(x^2-2\left(m-1\right)+2m-5=0\)
\(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-2m+1-2m+5=m^2-4m+6=\left(m-2\right)^2+2>0\forall m\)
\(\Leftrightarrow\) pt luôn có 2 nghiệm pb với mọi m
b/ Phương trình cớ 2 nghiệm trái dấu
\(\Leftrightarrow2m-5< 0\)
\(\Leftrightarrow m< \dfrac{5}{2}\)
c/ Theo định lí Vi - et ta có :
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1.x_2=2m-5\end{matrix}\right.\)
\(A=x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1.x_2\)
\(=4\left(m-1\right)^2-2\left(2m-5\right)\)
\(=4m^2-8m+4-4m+10\)
\(=4m^2-12m+14=4\left(m^2-3m+\dfrac{9}{4}\right)+5=4\left(m-\dfrac{3}{2}\right)^2+5\ge5\)
\(A_{min}=5\Leftrightarrow m=\dfrac{3}{2}\)
Đúng 2
Bình luận (0)
1, \(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-4m+6=\left(m-2\right)^2+2>0\)
Vậy pt luôn có 2 nghiệm pb với mọi m
2, Vì pt có 2 nghiệm trái dấu
\(x_1x_2=\dfrac{c}{a}=2m-5< 0\Leftrightarrow m< \dfrac{5}{2}\)
3, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)
\(A=\left(x_1+x_2\right)^2-2x_1x_2=4\left(m-1\right)^2-2\left(2m-5\right)\)
\(=4m^2-12m+14=4m^2-2.2m.3+9+6\)
\(=\left(2m-3\right)^2+6\ge6\forall m\)
Dấu ''='' xảy ra khi m = 3/2
Vậy với m = 3/2 thì A đạt GTNN tại 6
Đúng 4
Bình luận (1)
1: \(\text{Δ}=\left(2m-2\right)^2-4\left(2m-5\right)\)
\(=4m^2-8m+4-8m+20\)
\(=4m^2-16m+24\)
\(=4m^2-16m+16+8\)
\(=\left(2m-4\right)^2+8>0\forall m\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
2: Để phương trình có hai nghiệm trái dấu thì 2m-5<0
hay m<5/2
3: \(A=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(2m-2\right)^2-2\left(2m-5\right)\)
\(=4m^2-8m+4-4m+10\)
\(=4m^2-12m+14\)
\(=4m^2-12m+9+5\)
\(=\left(2m-3\right)^2+5\ge5\forall m\)
Dấu '=' xảy ra khi m=3/2
Đúng 1
Bình luận (0)